Implicit Differentiation and Inverse Functions

Return to Course Outline

Previous Lecture

Misc

Exam 1

Next Monday (March 11).

It will cover the things we’ve studied since the start of the semester (for example, limits including limit laws one-sided and infinite limits, when limits don’t exist; derivatives including the limit definition, differentiation rules, the chain rule; antiderivatives; etc.) Basically material covered by problem sets 1 through 4.

3 to 5 short-answer questions, similar to problem set questions except not immediately solvable by Mathematica or lookup.

Open book, notes, and online references. You can also use Mathematica and/or a calculator.

A sample test is now available.

SI Sessions

Friday (Mar. 8): 3:00 - 6:00, Bailey 209.

Questions?

Derivatives of Functions’ Inverses

Suppose you want to know what the derivative of arcsin is, i.e., what dy/dx is if y = arcsin x.

Rephrasing this as x = sin y gives you functions you know how to differentiate (namely sin), and you can use implicit differentiation to find dy/dx.

Start by differentiating both sides of the equation x = sin y:

Then isolate dy/dx:

Now you have dy/dx as a function of y. But since we started by wanting to find a derivative for arcsin x, it would be nicer to have the derivative in terms of x. The trigonometric identity sin²y + cos²y = 1 is the key to doing this:

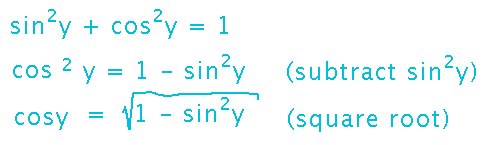
This doesn’t look all that helpful at first; it just turned cos y into a messier expression involving sin y. But notice that sin y = x, so the expression involving sin y is actually exactly what you need in order to express the derivative in terms of x:

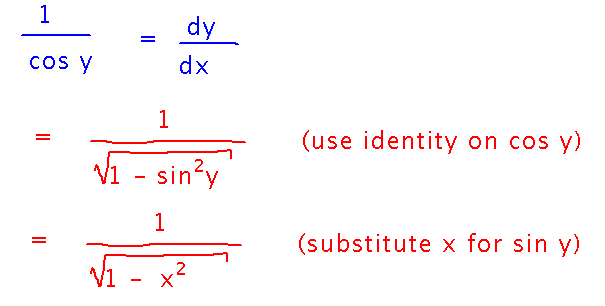
What we did here was

1. Differentiate both sides of the equation x = sin y.
2. Divide both sides by cos y to isolate dy/dx on one side.
3. Use a trigonometric identity to rewrite cos y in terms of sin y.
4. Replace sin y with x, justified by the original equation x = sin y.

This is a typical example of how you can often use implicit differentiation to find derivatives of the inverses of functions you already know how to differentiate.

Next

How to use information about one derivative to find a related one — “related rates” problems.

For example, I have an old silo on my property that casts a shadow in the morning sun. I’m curious how fast the length of the shadow (L) decreases as the sun rises:

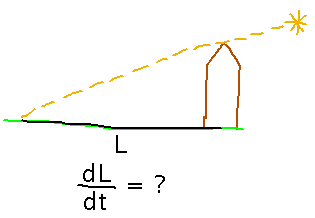
I’m too lazy to go measure the shrinking shadow, but I can figure out how fast the sun rises: Since it takes 24 hours to go 360 degrees around the Earth, it must move at a rate of 360/24 = 15 degrees per hour or 1/4 degree per minute.

If only there were some way to connect the length of the shadow to the sun’s angle.... And there is, because the shadow and the silo form two sides of a right triangle, so the tangent of the angle is the silo’s height divided by the length of the shadow (estimate the silo to be 30 feet high):

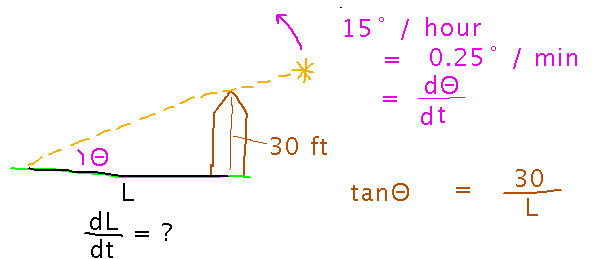
So now I can express L in terms of the angle, and thus the derivative of L in terms of the angle and its derivative:

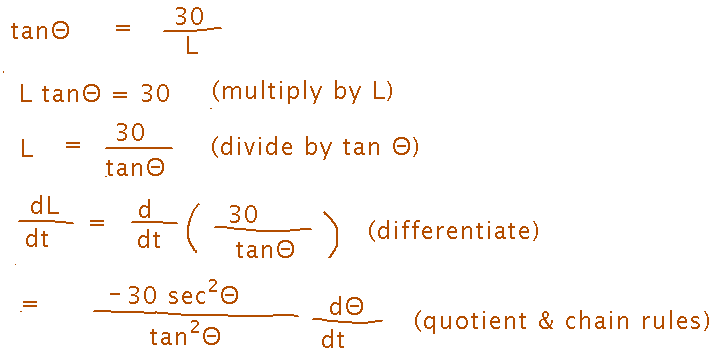
Finally, I can simplify by using the definitions of secant and tangent:

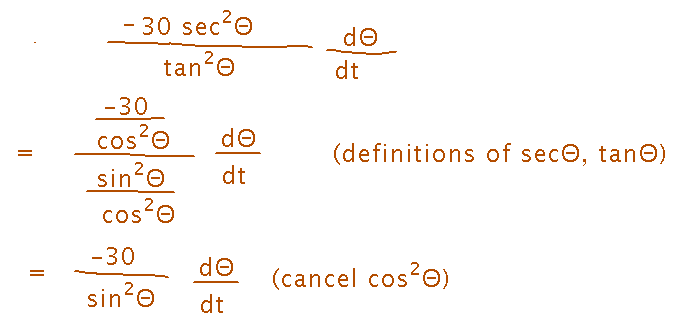
Thus I’ve found one rate of change (of the shadow) from another related one (of the sun’s position). Starting with knowledge of how fast the sun rises and how high the silo was, the steps were...

1. Express shadow length in terms of tan Θ
2. Differentiate to get an equation for dL/dt in terms of Θ and dΘ/dt
3. Use the definitions of sec Θ and tan Θ to simplify the equation.

This is a typical “related rates” problem.

For Wednesday, read section 4.1, the book’s discussion of related rates. Try to see how what we just did with the silo problem relates to what the book is talking about.

Next Lecture