SUNY Geneseo Department of Mathematics
Thursday, March 7
Math 221 03
Spring 2019
Prof. Doug Baldwin
Marcus Elia, “Fast Polynomial Multiplication for Cryptography”
Wednesday, March 13, 4:00 - 5:00 PM
Newton 201
Up to 2 problem set points of extra credit for going and writing a paragraph of connections you make to the talk.
Next Monday (March 11).
It will cover the things we’ve studied since the start of the semester (for example, limits including limit laws one-sided and infinite limits, when limits don’t exist; derivatives including the limit definition, differentiation rules, the chain rule; antiderivatives; etc.) Basically material covered by problem sets 1 through 4.
3 to 5 short-answer questions, similar to problem set questions except not immediately solvable by Mathematica or lookup.
Open book, notes, and online references. You can also use Mathematica and/or a calculator.
A sample test is now available.
Friday (Mar. 8): 3:00 - 6:00, Bailey 209.
Section 3.7.
Find dy/dx if x2 - y2 = 1.
Yesterday we had figured out how to differentiate both sides of the equation together. This is one of two main stages to solving any implicit differentiation problem.
The second stage is to rearrange the equation to isolate dy/dx on one side:
Question: is that derivative really a slope; how would you use it?
Yes it is a slope. If you think of a tangent line that touches the curve at point (x,y), that line has slope x/y.
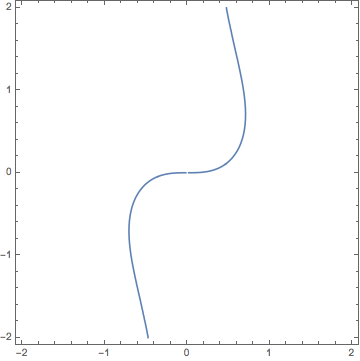
Find dy/dx if x2 + y2 = y/x.
What does this equation look like? Use the ContourPlot function to plot implicit curves with Mathematica. See this notebook for some examples.
Find the derivative. Start by differentiating both sides of the equation:
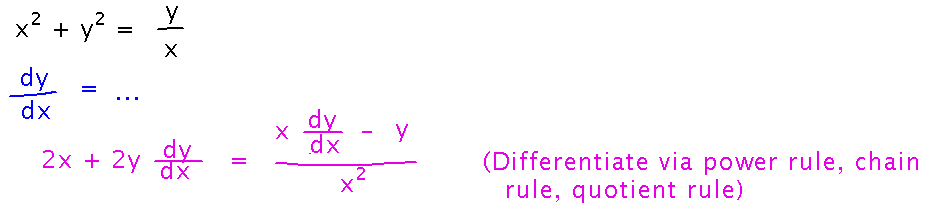
Then rearrange terms to isolate dy/dx on one side:
Do derivatives always have to be dy/dx? Could they be dx/dy? What would that mean?
They can indeed be dx/dy. Calculate them by implicit differentiation much as you would dy/dx, just remember that it’s the x terms you need to use the chain rule on. As a slope, dx/dy is the amount x has to change by to produce a unit change in y (vs dy/dx which is how much change in y a unit change in x produces).
Suppose y = arcsin x = sin-1 x. Can you find dy/dx?
Yes. The trick is to realize that if y = arcsin x then x = sin y, and in that form you know how to differentiate everything. The obvious derivative you’d get would be dx/dy, but if you treat x = sin y as an equation to be differentiated implicitly you can find dy/dx instead.
Finish the inverse (arcsin) example.
Then start looking at related rates problems.
Start reading section 4.1.