SUNY Geneseo Department of Mathematics

Implicit Differentiation, Part 2

Wednesday, March 6

Math 221 03
Spring 2019
Prof. Doug Baldwin

Misc

Exam 1

Next Monday (March 11).

It will cover the things we’ve studied since the start of the semester (for example, limits including limit laws one-sided and infinite limits, when limits don’t exist; derivatives including the limit definition, differentiation rules, the chain rule; antiderivatives; etc.) Basically material covered by problem sets 1 through 4.

3 to 5 short-answer questions, similar to problem set questions except not immediately solvable by Mathematica or lookup.

Open book, notes, and online references. You can also use Mathematica and/or a calculator.

Sample test coming soon.

SI Sessions

Friday (Mar. 8): 3:00 - 6:00

Questions?

Oil Slick from Problem Set?

A more detailed explanation of how to solve this problem:

Start with the formula for the area of an ellipse.

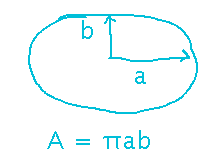
Ellipse with semi-major axis a and semi-minor axis b has area pi times a times b

Now, you need to find the derivative of the area with respect to time. Note that the area is a product of two quantities (a and b) that are both changing with time. So you can use the product rule to differentiate area:

Use product rule to express derivative of area in terms of a, b, and their derivatives

Unlike other problems you’ve seen, this one doesn’t have formulas you can plug in for da/dt, a, etc. Instead, it has actual numbers:

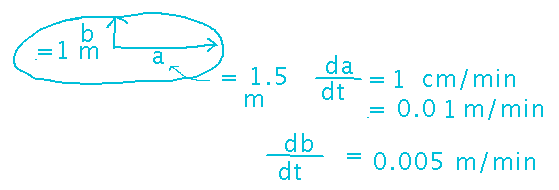
Ellipse with values for a, b, and their derivatives

So plug these numbers in to get a number for how fast area is changing.

For the second part of the problem, how fast is volume changing, you can do something similar, except that since thickness doesn’t change, you just need to use the constant multiple rule, not the full product rule:

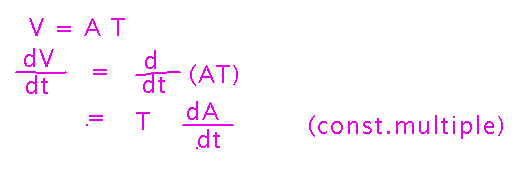
Derivative of volume is thickness times derivative of area

Once again, the problem gives you a number for thickness (T), and the answer to part A gives you dA/dt.

Quotient with Product Rule?

Go over the third differentiation problem from the problem set?

The direct way to solve it is to treat it as a product involving a quotient, and so use the product and quotient rules to find the derivative. (You could also multiply the (t+1) term and the numerator from the quotient by hand, and end up with something that just needs you to use the quotient rule). Once you’ve used these 2 rules, quite a bit of simplification is possible.

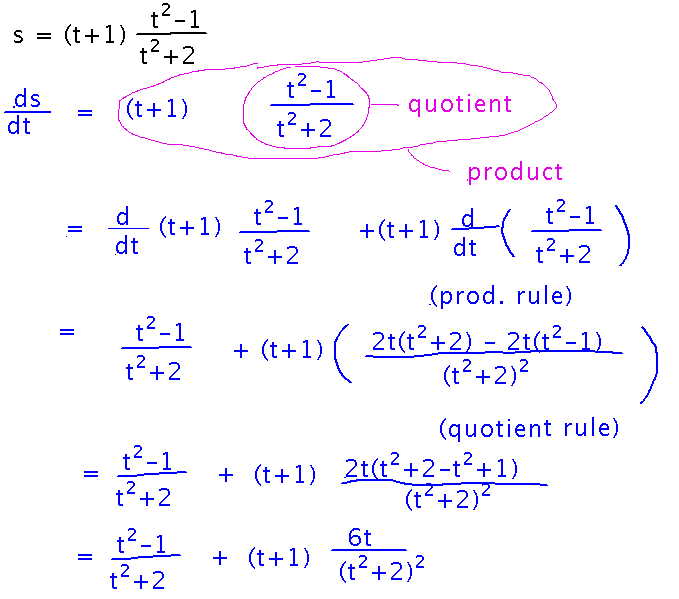
Using the quotient rule to differentiate one term in a product

Second Derivative?

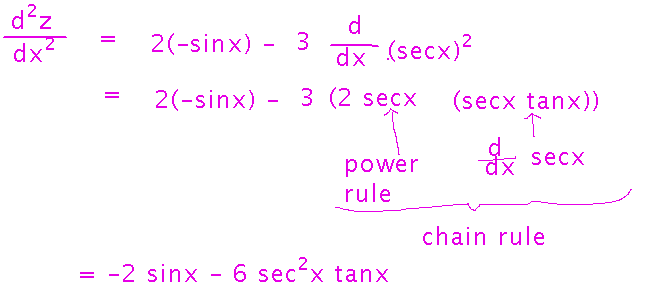
Go over the first of the second derivative questions from the problem set?

To find a second derivative, you need a first derivative to start with. In this case, you can find that derivative from the derivatives of the standard trig functions, and the constant multiple and difference differentiation rules:

The derivative of 2 sine x minus 3 tangent x is 2 cosine x minus 3 secant squared x

Then differentiate the first derivative to find the second derivative. This also uses the difference and constant multiple rules, along with the chain rule to differentiate sec²x. The result from those rules can be simplified a little.

Differentiating 2 cosine x minus 3 secant squared x via the chain rule among other rules

Implicit Differentiation

Example from Last Time

Find dy/dx if x² - y² = 1.

Last time, we ended with the idea that you “start with the implicit equation.” What does this mean?

It means you can start by simply differentiating both sides of the equation. To do this, you need to use the chain rule every time you differentiate a term involving y, since it’s implicitly a function of x:

Implicit differentiation starts by differentiating both sides of an equation, using the chain rule

More examples of implicit differentiation.

See if you can finish the x² - y² = 1 example for tomorrow.

Next Lecture