Misc
Exam 1
Next Monday (March 11).
Covers material since the start of the semester (e.g., limits, derivatives as limits, differentiation rules, chain rule).
4 - 6 short-answer questions.
Open-calculator, open-book, open-notes, open-computer for reference or Mathematica.
I will share a practice test.
Problem Set
See handout for details.
Discussion
Congratulations on doing it well.
Key points:
- Examples of some applications of calculus.
- Example of an initial value problem and how to solve such problems.
Questions?
Is the elliptical oil slick question on the problem set an implicit differentiation question? A chain rule question?
None of the above it. It’s a product question:
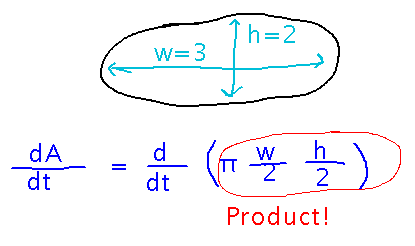
Implicit Differentiation
Section 3.7.
Motivation
Normally you see functions given in “explicit” form, i.e., they provide an explicit equation for calculating y from x. You can then use the differentiation rules we’ve studied to find the derivative of y. However, you can also define functions “implicitly,” i.e., by writing some equation that implies some relationship between the values of variables.
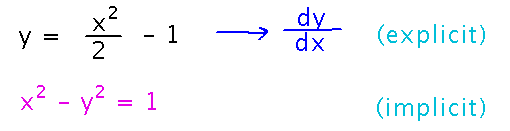
Does it even make sense to talk about derivatives when all you have is an implicit equation? For instance, here’s a graph of solutions to x2 - y2 = 1, which shows that the equation doesn’t even define a function (since there are multiple values of y for some x values).
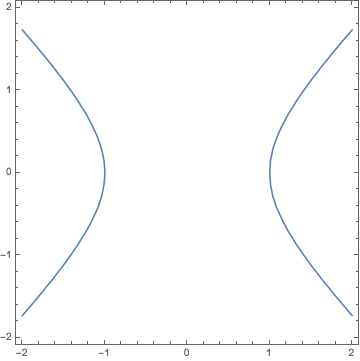
But nonetheless, such curves do have tangent lines, which have slopes, and if you think of derivatives as slopes of tangent lines, then apparently it does make sense to think about derivatives of implicit curves.
Can you turn an implicit representation into an explicit one? Sometimes, although you have to be careful not to lose information in places where the implicit equation has multiple y values for a single x. For example, you can rearrange x2 - y2 = 1 like this:
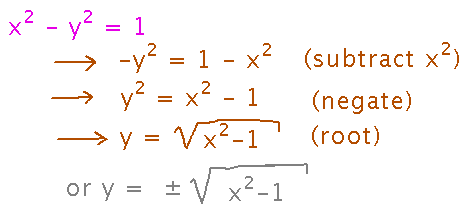
Finding Derivatives
Start with the implicit equation (don’t put into explicit form)
We’ll look at what comes next on Wednesday. In the mean time, re-read (parts of) section 3.7 to see if you can figure out what “start with the implicit equation” means in practice and how to do it.
Next
Finish implicit differentiation.