Derivatives of Trigonometric Functions, Part 1

Return to Course Outline

Previous Lecture

Misc

Only 1 of the 2 pages of problem set 3 was copied in the original handout.

The handout in Canvas has always had both pages, and a corrected paper version is available for anyone who wants it.

Questions?

How to take a derivative with Mathematica? Use the D function — see the examples here and in the Feb. 15 lecture.

Derivatives of Trigonometric Functions

Section 3.5.

Cosine

The book proves that the derivative of sinx is cosx, and asserts that the derivative of cosx is -sinx but leaves the proof/derivation to the reader.

Let’s do that proof.

Pretty much the only way we can start, since we don’t have differentiation rules for trig functions, is to fall back on the limit definition of derivative:

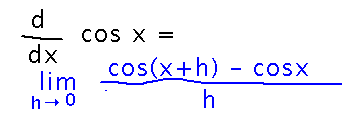
Now we can remember that there’s an identity for the cosine of the sum of two angles (and look that identity up if need be):

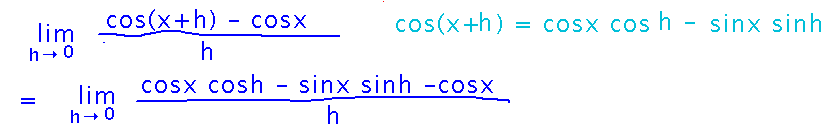
Next we can separate the terms involving cosine from the terms involving sine.

By using the difference and product limit laws, we can turn the big limit into 4 simpler ones. Two of these limits are ones to which the squeeze theorem applies, and the other two are easy to evaluate because the functions in question don’t depend on h at all:

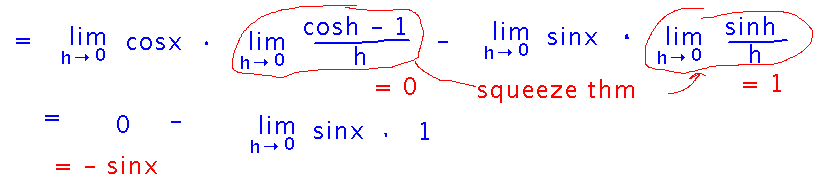
Tangent, Etc.

Now that we have derivatives for sine and cosine, the other trigonometric functions are easier, because they’re ultimately defined in terms of sine and cosine.

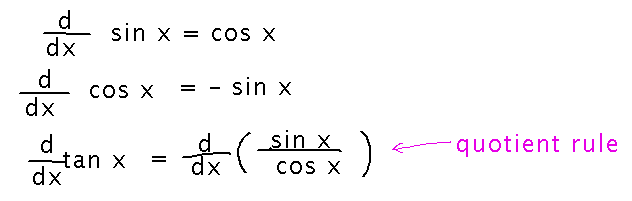
See the textbook for a complete list.

Next

Look at derivatives of other trig functions, and practice finding derivatives and antiderivatives of expressions involving trig functions.

Next Lecture