Misc
SI session this afternoon (3:00, Bailey 209)
Questions?
Trigonometric Derivatives
Section 3.5.
Functions other than Sine and Cosine
What’s the derivative of sec x?
This is an example of how you can differentiate trig functions other than sine and cosine by defining the function in terms of sine and cosine and then using the quotient rule.

Specifically...
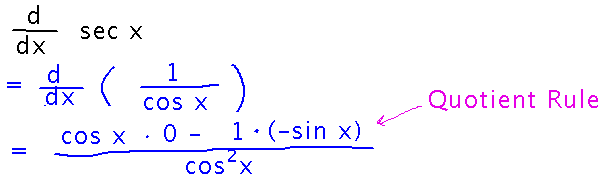
From here, you can rearrange terms to simplify:
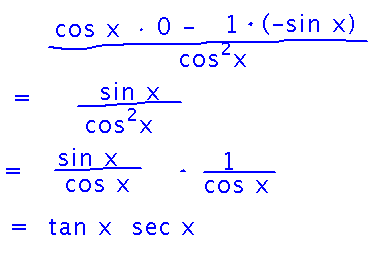
Practice
Find dy/dx if y = 3sinx - 2cosx
This mostly draws on old rules (the constant multiple rule, difference rule), plus the derivatives of sine and cosine.
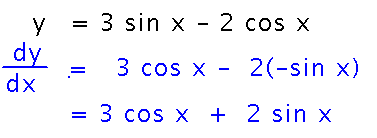
How about the antiderivative?
Start with some antiderivative rules very analogous to differentiation rules, e.g., constant multiple, difference:
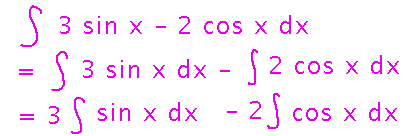
Now we have to figure out what the antiderivatives of sine and cosine are. Cosine is relatively easy, since we already know it’s the derivative of sine, so sine (+ a constant) is the antiderivative of cosine. For the antiderivative of sine, we can reason that if negative sine is the derivative of cosine, then maybe sine is the derivative of negative cosine. And of course we can check this guess and find that it’s right:
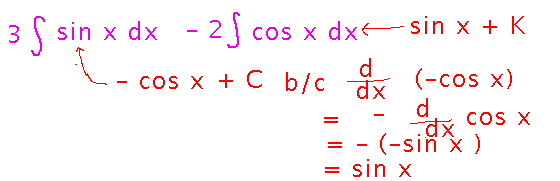
With these ideas, finding the rest of the antiderivative is mostly a matter of plugging them in and simplifying:

Find f′(x) if f(x) = secx tanx
This is mainly a matter of using the product rule for derivatives:

But it simplifies further:
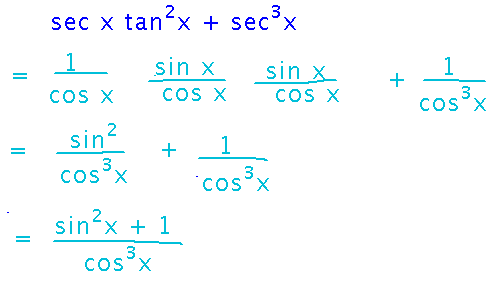
Next
Nothing we’ve done so far would allow you to, for example, differentiate sin(3x).
Derivatives of functions applied to other functions require the so-called “chain rule.”
Read about it, and think about how you’d differentiate sin(3x).
Section 3.6.