Misc
SI session this afternoon, 3:00.
Questions?
Differentiation Laws
Section 3.3.
Example
Find the derivative of 5x2 - 2x.
Simple answer: 10x - 2.
This comes from applying a series of rules for evaluating derivatives, individually dealing with simple patterns but working together on more complicated expressions such as this one.
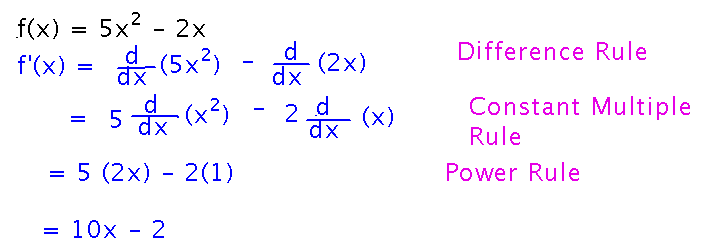
Mathematica
Mathematica can take derivatives using the D function.
Mathematica’s presentation of the results is sometimes not what a person would expect. The Simplify function sometimes puts results into more recognizable forms.
Here is a Mathematica notebook with some examples.
More on the Power Law
Differentiate x4 + 7x2 - 12 + x-1.
This is much like the previous example, except noticing that the power rule applies to negative powers as well as positive ones (and technically using a sum rule along with the difference rule):
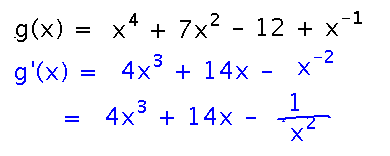
Notation and 2nd Derivatives
Find dy/dx if y = 7x3 + x2 - 7x.
This introduces another notation for derivatives, but otherwise works like the earlier examples.

Now what about d2y/dx2? This notation means the “2nd derivative,” i.e., the derivative of the derivative.
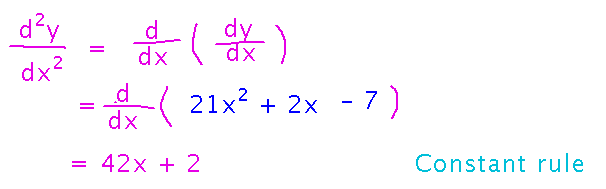
Why would you care about second derivatives? Remember our Galileo scenario, wanting to know the instantaneous speed of a rolling ball from information about its position. We simplified Galileo’s discovery by assuming units of distance and time in which position is equal to time squared.
We also know by now that the since speed is the rate at which distance changes, the instantaneous speed is the derivative of position. And moreover, the rate of change of speed is acceleration, so it’s the derivative of speed, and thus the second derivative of position:

(You can even go one derivative further: the rate of change of acceleration is called “jerk,” so jerk is the third derivative of position.)
Problem Set
...on derivatives, specifically the limit definition and differentiation rules.
See the handout for details.
Next
Differentiation rules for handling products and quotients.
Finish reading section 3.3.