The Product and Quotient Rules

Return to Course Outline

Previous Lecture

Questions?

The Product and Quotient Rules

Part of section 3.3.

Product Example

Find dy/dx if y = (x² + 3)(x-2)

This is a product, so we can use the product rule on it:

Double check: we could also just multiply out the product before differentiating, and then use the familiar power rule, etc.

Simple Quotient Example

Find dy/dx if y = 1 / (x²-1)

This is a quotient of two terms (although the numerator is very simple), and so we can use the quotient rule to differentiate it. The quotient rule is similar to the product rule, although with subtraction (which means the order of the terms matters), and a division.

Another Quotient Example

Find g′(x) if g(x) = (3x - 1) / (x² + 6x)

This involves more complicated derivatives, but still uses the quotient rule:

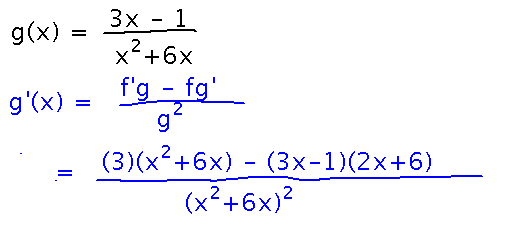
We can simplify this basic quotient rule result somewhat:

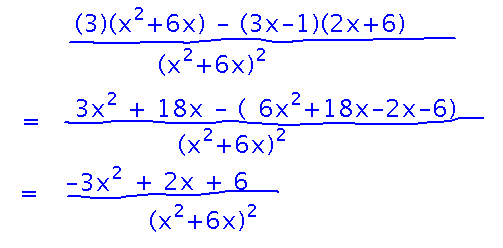
Antiderivatives

With rules for finding various derivatives, we can also ask the opposite question: if I have a function, what might it be the derivative of?

For example, find a function f(x) such that f′(x) = 3x

But notice that there are many such functions, differing by what constant appears at the end. For the most general form, use “C” to stand for an arbitrary constant.

What you just found is called an “antiderivative.” Many of our differentiation rules lead to corresponding antidifferentiation rules, for example a power rule, a constant multiple rule, sum and difference rules, etc.

Next

Ultimately, derivatives of trigonometric functions.

But in order to do that, we need some more tools for limits.

Read “The Squeeze Theorem” in section 2.3.

Next Lecture