SUNY Geneseo Department of Mathematics

The Limit Definition of Derivatives

Thursday, February 14

Math 221 03
Spring 2019
Prof. Doug Baldwin

Misc

Grow STEM ice cream social.

Feb. 20, 6:30 PM, Newton 209.

Grow STEM is a student/faculty group interested in promoting diversity in STEM fields; this event is a chance to meet them and learn more about what they do.

Questions?

Derivatives

Section 3.1.

Example

What is the derivative of f(x) = 4 - x² at point (2,0)?

See the book’s formula for a derivative at a given x value. And in fact, by treating x as a variable instead of plugging in a specific number for it, the same formula gives us a way to find derivatives as functions.

The basic idea is that a derivative is a slope, namely between points (x, f(x)) and (x+h, f(x+h)) — in the limit, as h goes to 0, which makes the derivative, f′(x), equal to the slope of the tangent line at (x, f(x)).

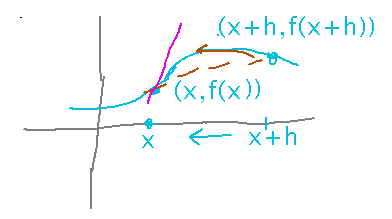
Graph of a curve between (x,f(x)) and (x+h,f(x+h)) with h getting closer to 0

Set up the limit for the example function:

For f(x) = 4-x^2, the derivative at 2 is the limit as h approaches 0 of 4-(x+h)^2 - (4-x^2) all over h

To evaluate this limit, expand the (x+h)² term, and notice that lots of things then cancel out in the numerator:

The 4 and x^2 terms after squaring (x+h) cancel

Furthermore, all the terms left in the numerator have an h, which cancels with the h in the denominator:

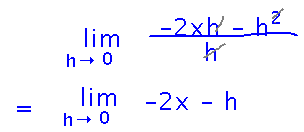
Limit of -2xh - h^2 all over h simplifies to limit of -2x - h

Now we can plug in h = 0 and get the derivative in terms of x. Recalling that we were interested in x = 2 gives us a numeric value of the derivative at point (2,0):

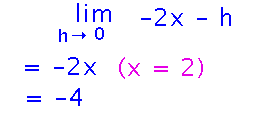
Limit of -2x - h becomes -2x, or -4 when x = 2

Visually, this “-4” is the slope of the tangent to f(x) at (4,0). The negative sign means the tangent line goes down as x increases. The general formula f′(x) = -2x gives us a formula for the derivative at any x value:

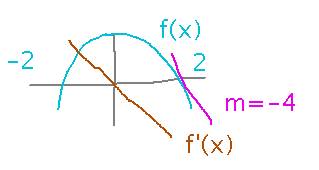
Graph of 4 - x^2 with downward-sloping tangent at (2,0) and graph of derivative as downward-sloping line through origin

Generalizing

Many of you knew that a “bring the exponent down and subtract one” rule also gives the derivative, with considerably less work than using the limit definition. This is one of many derivative rules, i.e., formulas that let you jump straight to results of limits rather than having to evaluate them by hand.

Let’s see if we can work out where it comes from, by using the limit definition to differentiate a generic power, xⁿ:

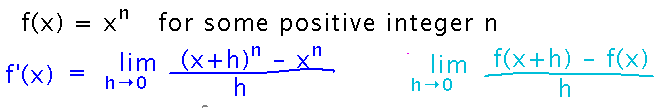
Limit as h approaches 0 of (x+h)^n - x^n all over h

You have to take on faith a formula for expanding (x+h)ⁿ, namely...

(x+h)^n expands to sum of terms involving binomial coefficients, decreasing powers of x, and increasing powers of h

Now things get simpler fast, because the xⁿ terms in the numerator cancel out:

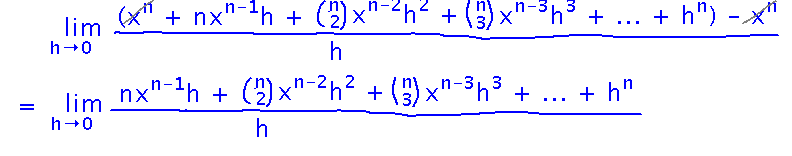
Sum of terms with x^n and -x^n cancelled

And everything that’s left has a factor of h, which cancels with the denominator:

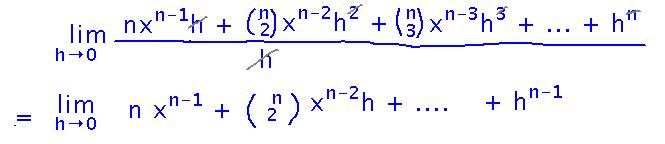
Limit of sum of terms with h cancelled against denominator

And finally we can plug h = 0 in to this expression, which zeros every term except n x^n-1:

Limit of sum becomes n x^(n-1)

Key Points

We did a lot today, in particular...

The definition of the derivative as a limit

The use of that definition to derive a rule for finding certain derivatives without explicitly taking a limit. (Like the formal definition of limit could be used to prove limit laws, the main value of the limit definition of derivatives is in proving differentiation rules that are easier to use than the formal definition is.)

Differentiation rules.

Read section 3.3

Next Lecture