SUNY Geneseo Department of Mathematics
Monday, December 9
Math 221 06
Fall 2019
Prof. Doug Baldwin
4 of you have filled them out now. Thank you!
Others, please do fill one out, the feedback helps me with future courses.
A sample exam is available in Canvas, both without solutions and with solutions.
Wednesday, December 11, 8:00 - 11:20 AM, in our South Hall classroom.
Comprehensive, but concentrates on material since the second hour exam (problem sets 9 through 13, e.g., optimization, L’Hospital’s rule, summations, integrals, the Fundamental Theorem, areas, volumes, etc.)
Designed for about 2 hours, you’ll have 3 hours 20 minutes.
Rules and format otherwise similar to hour exams, especially open-references rules.
I’ll bring donuts and cider.
3-hour SI today (Dec. 9), 3:00 - 6:00, Fraser 104.
1 hour tomorrow (Tuesday, Dec. 10, study day), 12:00 - 1:00, in our regular classroom. Bring questions or topics you want to go over.
Wednesday, December 11 (i.e., final exam day).
Please turn in any extra credit you want counted in your grade by then.
Please also complete any late grading appointments by then.
(Left from last time.)
What is the volume of the bowl produced by rotating y = x2 around the y axis, for 0 ≤ y ≤ 1?
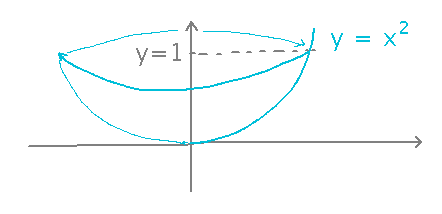
Express the curve as a function of y, then you can use the standard “integrate volume of disks” method with y as the variable to find the volume of revolution around the y axis.
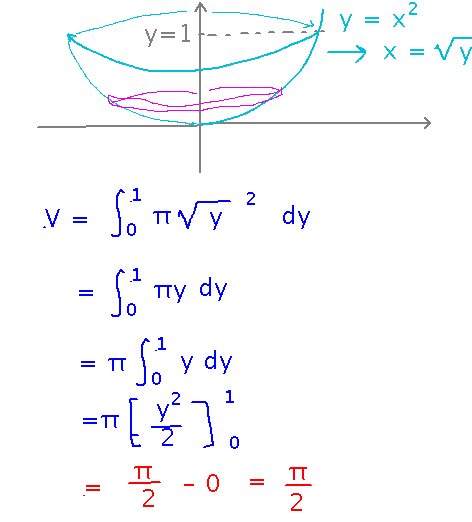
Key Idea: You can rotate around y, if you phrase the function and integral in terms of y.
Example (similar to example 6.10): What is the volume produced by rotating the region between f(x) = x and g(x) = x2 for 0 ≤ x ≤ 1 around the x axis?
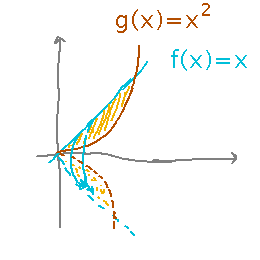
Key insight is that you can still think of “disks” produced by rotating the curve around the axis, but now they have holes in them. Their areas are thus the difference of the area of the hole (the inner circle, corresponding to the smaller function) and the whole disk (the outer circle, corresponding to the larger function).
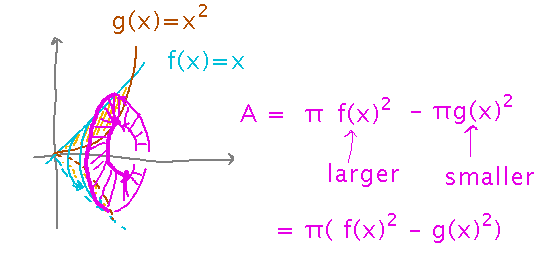
Applying this idea to the example proceeds much like other slice problems, once you realize the “difference of circles” trick for calculating cross section area.
