SUNY Geneseo Department of Mathematics

Review

Tuesday, December 10

Math 221 06
Fall 2019
Prof. Doug Baldwin

Sample Exam Question 5

Block rotating on a turntable, but seen from the side. The question gives you equations that relate x (the apparent side-to-side position of the block) to Θ (the rotation of the turntable) and Θ to t (time). You need to find dx/dt.

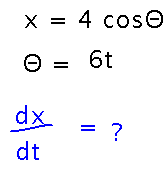
x equals 4 cosine theta; theta equals 6 t; what is d x over d t?

The key thing is to see a way to combine the information about x and Θ, e.g., plug the equation for Θ in terms of t into the equation for x. Once you do that, you can differentiate using the constant multiple and chain rules:

x equals 4 cosine of 6 t, so d x over d t is minus 24 sine of 6 t

Sample Exam Question 3

Solving an equation for b, where b is a bound on an integral. Expanding the integral into an antiderivative evaluated at the two endpoints gives you a more conventional-looking equation, which you can solve using conventional means:

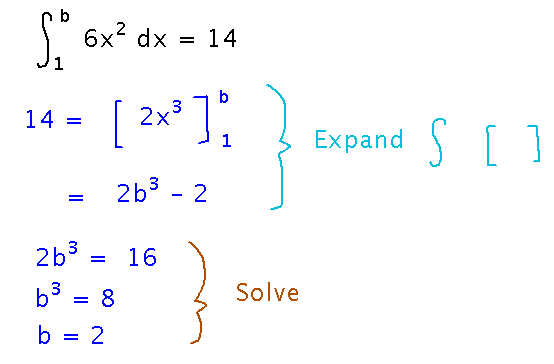
To find b such that integral from 1 to b of 6 x squared is 14, expand the integral, then solve for b

Related Rates

Try some examples from the textbook.

Ladder on Wall

A ladder that is leaning against a wall slides down it in such a way that its top slides down at a rate of 2 feet/second. How fast is the bottom moving when it is 5 feet away from the wall?

Start by giving names to the relevant quantities, and figuring out where you want (or have) their derivatives:

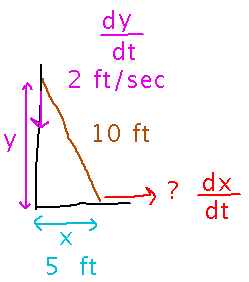
Ladder leaning on wall with top y feet up and bottom x feet out, top slides 2 feet per second

Now come up with equations that relate the values you know to the one(s) you need. In this case the key idea is that the ladder, wall, and ground form a triangle on which you can use the Pythagorean Theorem. Implicit differentiation then gives you an equation involving dx/dt:

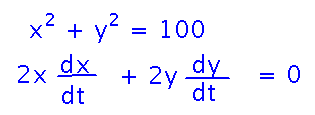
x squared plus y squared equals 100, so 2 x times d x d t plus 2 y times d y d t equals 0

Rearrange this equation to get dx/dt alone on one side, then plug in known numbers for the other quantities. Or, in the case of y, a quantity you can calculate from the ones you know.

Solving for d x d t gives 2 times radical 3

Note that it paid to be careful about the signs of things in this problem. Before we realized that dy/dt is negative, even though the prose problem description doesn’t explicitly say so, we were getting an unintuitively negative value for dx/dt.

A Problem Involving Angles

Two adjacent sides of a triangle have lengths 3 feet and 5 feet. The angle between them is changing at a rate of 0.1 radians/second. How fast is the area of the triangle changing when the angle is π/6 radians?

As before, start by diagramming the situation, assigning names to the quantities of interest, and figuring out where the derivatives are:

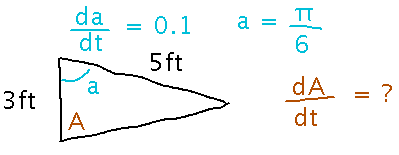
Triangle with sides of length 3 and 5, angle a between them with d a d t equal to 0.1

In this problem, the formula for the area of a triangle (area = base times height over 2) is a good place to start connecting what you know about the changing angle to what you want about the changing area. But in order to use that formula, you need the height of the triangle, which you can get from the angle thanks to the definition of the sine function:

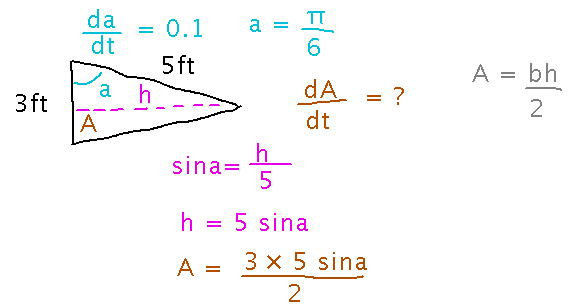
h is perpendicular distance from apex to length 3 side, so h is 5 times sine a

Now you have an explicit equation for area, so you can just differentiate it and plug in numbers:

d A d t equals 15 halves times cosine a times d a d t which equals about 0.6495 square feet per second

Sample Exam Question 2

Alternative substitutions for evaluating the integral of 4 sin(2x) cos(2x).

The solution offers u = sin(2x) and u = cos(2x) as the two possible substitutions. Why not consider u = 2x also?

You could, but it would have to be followed by a second substitution involving either sinu or cosu. So I focused on single substitutions that would let you solve the whole integral in my solution.

(No Next Lecture)