SUNY Geneseo Department of Mathematics

Volume by Slicing

Thursday, December 5

Math 221 06
Fall 2019
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

Differential Equations Experiment

Two students trying to measure whether a web animation they developed helps students learn differential equations.

Looking for volunteers who have taken calculus 1 (you count) but not differential equations (you still count) to participate in an experiment.

Either stop by South 347 in one of the following times

or contact Sal Galarza or Jack Truckenmiller for more information.

Takes about 1 1/2 hours.

SI

Today, 3:00 - 4:30, Fraser 104

Last regular SI meeting

SOFIs

Thank you to the one person who has filled one out!

Others, please fill one out for this course, the feedback helps me with future courses.

Final Exam

A sample exam is available in Canvas, both without solutions and with solutions.

Wednesday, December 11, 8:00 - 11:20 AM, in our South Hall classroom.

Comprehensive, but concentrates on material since the second hour exam (problem sets 9 through 13, e.g., optimization, L’Hospital’s rule, summations, integrals, the Fundamental Theorem, areas, volumes, etc.)

Designed for about 2 hours, you’ll have 3 hours 20 minutes.

Rules and format otherwise similar to hour exams, especially open-references rules.

I’ll bring donuts and cider.

Review Sessions

3-hour SI next Monday (Dec. 9), 3:00 - 6:00, Fraser 104.

1 hour on study day (Tuesday, Dec. 10), 12:00 - 1:00, in our regular classroom. Bring questions or topics you want to go over.

Last Day for Grading

Wednesday, December 11 (i.e., final exam day).

Please turn in any extra credit you want counted in your grade by then.

Please also complete any late grading appointments by then.

Questions?

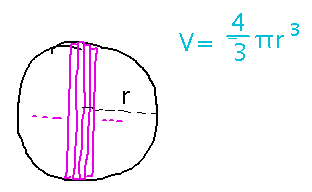
Problem set question re volume of sphere?

The goal is to use the slice method to derive the formula for the volume of a sphere. So you know the formula you’re working towards.

The first step is to find a way to divide the sphere into slices whose cross-section area you know (area because volume is then just area times thickness, which is dx in the eventual integral). Maybe vertical circular slices would work...

A sphere split into thin vertical slices; V equals 4 thirds pi r cubed

Now you need to work out the volume of the slice at distance x from the center of the sphere. The Pythagorean Theorem helps, because the distance x, the radius of the slice, y, and the radius r of the sphere are the sides and hypotenuse of a triangle.

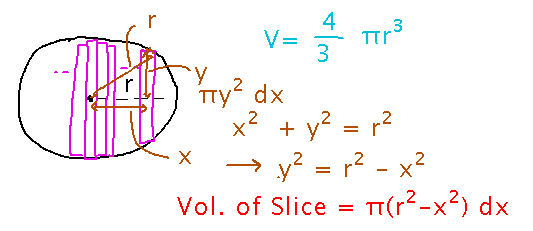
Slice of sphere as vertical side of right triangle; volume of slice is pi times r squared minus x squared, all times d x

Now that you have a formula for the volume of a slice, integrate it over all possible x values. In this case that’s -r (the left side of the sphere) to r (the right side).

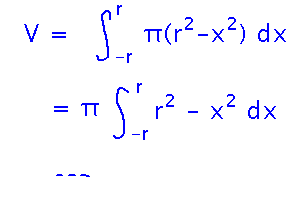
Integral from minus r to r of pi times the quantity r squared minus x square d r

Volumes by Slices

Section 6.2.

Key Idea(s)

Procedure

  1. Divide volume into thin shapes whose area you can calculate
  2. Theory: Sum area times thickness over interval that contains the volume, take limit as thickness approaches 0. This is the limit of a Riemann sum, leading to...
  3. Practice: Integrate areas over interval that contains the volume.

Example

Finish pyramid

Pyramid on its side, width and height of cross section are x over 2

Each slice has cross-section area (x/2)2. One way to integrate that is to use a u-substitution:

Integrate x over 2 squared from 0 to 2 via substitution u equals x over 2, result is 2 thirds

Or, that substitution might be overkill when you can just expand (x/2)2 and integrate directly:

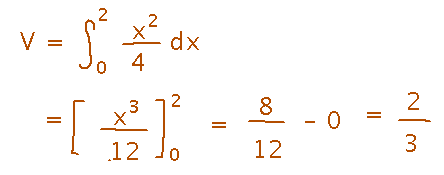
Integrate x over 2 squared from 0 to 2 as x squared over 4, result is 2 thirds

But both methods produce the same answer, and whichever seems most natural to you is fine.

Next

Another slice example

Volumes of revolution

Maybe slices as “washers”

Read “The Disk Method” in section 6.2.

Next Lecture