Misc
SOFIs
…are now under way.
Please fill one out for this course, the feedback helps me with future courses.
Final Exam
Wednesday, December 11, 8:00 - 11:20 AM, in our South Hall classroom.
Comprehensive, but concentrates on material since the second hour exam (problem sets 9 through 13, e.g., optimization, L’Hospital’s rule, summations, integrals, the Fundamental Theorem, areas, volumes, etc.)
Designed for about 2 hours, you’ll have 3 hours 20 minutes.
Rules and format otherwise similar to hour exams, especially open-references rules.
I’ll try to post some sample questions.
Donuts and cider.
Review Sessions
3-hour SI next Monday (Dec. 9), 3:00 - 6:00, Fraser 104.
1 hour on study day (Tuesday, Dec. 10), 12:00 - 1:00, in our regular classroom. Bring questions or topics you want to go over.
Last Day for Grading
Wednesday, December 11 (i.e., final exam day).
Please turn in any extra credit you want counted in your grade by then.
Please also complete any late grading appointments by then.
Questions?
Area between Curves
We looked at the basic idea last class: if f(x) ≥ g(x) for a ≤ x ≤ b, then the area between the graphs of f(x) and g(x) in the interval a ≤ x ≤ b is the integral from a to b of f(x) - g(x):
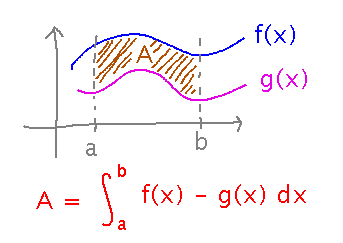
Section 6.1.
One Detail
Find the area between the graphs of y = sin x and y = cos x between x = 0 and x = π.
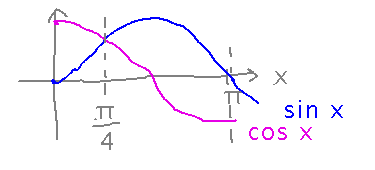
The problem here is that neither function is consistently bigger than the other. The graphs cross at x = π/2. So much as happened when finding the area between a graph and the x axis if the function was sometimes negative, break the integration into several integrals over partial intervals, and switch the order of the subtraction in order to always subtract the smaller function from the larger.
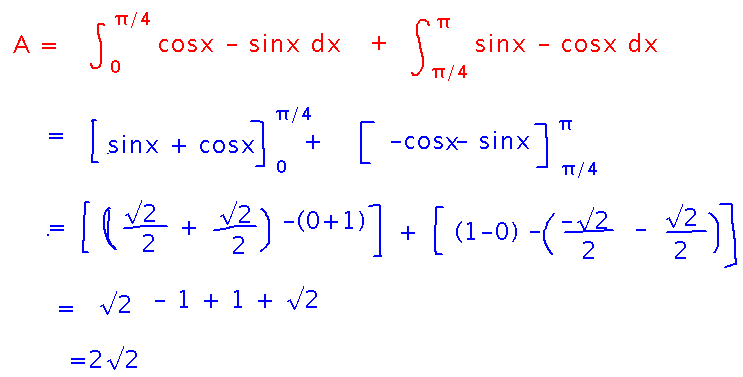
Key Idea
You always need to subtract the smaller function from the larger, so split the interval if necessary.
Another way to think of this is that you always integrate | f(x) - g(x) |.
Next
Volumes by slicing.
For example, what is the volume of this pyramid lying along the x axis:
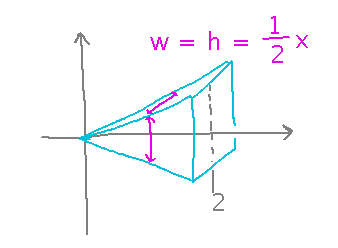
If you split the tapered pyramid into lots of thin slices, you can think of each slice as having a constant height and width, and calculate its volume by multiplying length times width times height:
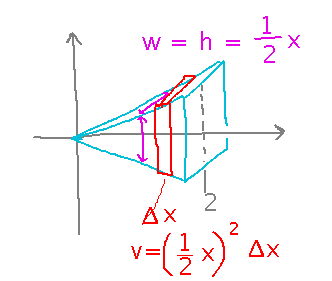
Now approximate the volume of the whole pyramid by adding the volumes of all the slices:
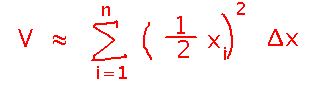
This is an approximation, but it gets more accurate as the slices get thinner. So in the limit, as you have an infinite number of infinitely thin slices, you get the exact volume.
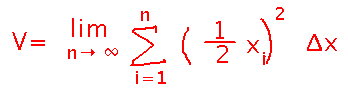
And this limit is just a limit of a Riemann sum, i.e., a definite integral!
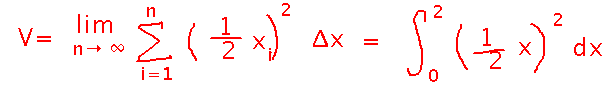
This example gives you a sense of how volume can be described by a Riemann sum, and thus an integral. Tomorrow we’ll look at it a little more generally, and do some more examples.
Read section 6.2.