Substitution in Definite Integrals

Return to Course Outline

Previous Lecture

Misc

No SI today.

Questions?

Substitution and Definite Integrals

“Substitution for Definite Integrals” in section 5.5.

Key Idea(s)

Apply substitutions to an integral’s bounds as well as to its integrand.

Examples

(Based on example 5.35)

Evaluate the integral from 0 to 2 of x e^x2-1.

Preliminary question: Where does the “1/8” come from in example 5.35? It’s because after doing the substitution, du is 8 times bigger than what it has to correspond to in the original integrand:

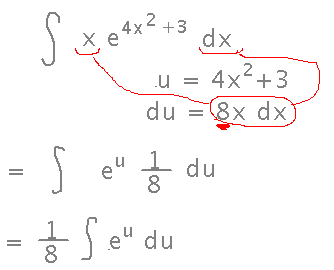
Do a similar substitution in x e^x2-1. Remember to apply it to the bounds of the integral:

Evaluate the integral from 0 to π/4 of 2 cos(2x) / (1 + sin²(2x)).

Hint: the antiderivative of 1 / (1+t²) is tan^-1t.

The first way of doing this is to do the single substitution u = sin(2x).

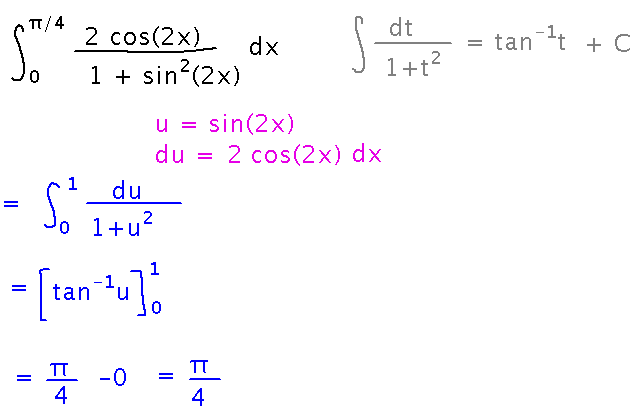
You can also do it in a series of 2 simpler substitutions. In this case you apply the substitutions to the bounds at each step. This process reaches the same final substitution that the single substitution did, and thus the same final answer.

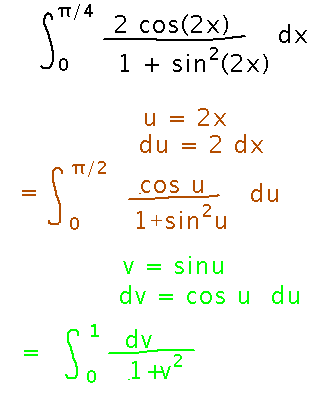
Problem Set

On substitution and area/volume applications of integrals.

See handout for details.

Next

Applications of integration: area between curves.

The key idea is that the area between 2 curves can be found by integrating the difference of the corresponding functions. (Formally, think of the area as a series of rectangular slices, whose heights are the difference of the functions -- a Riemann sum.)

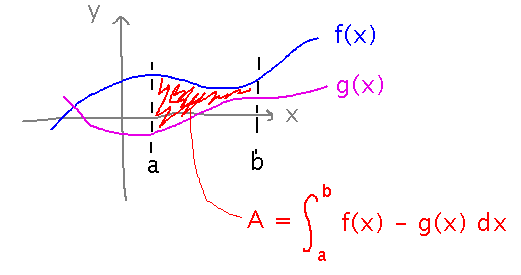
For example, find the area between the graphs of y = x and y = x², for 0 ≤ x ≤ 1:

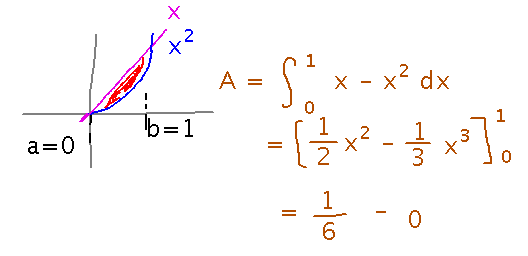
Read section 6.1.

Next Lecture