SUNY Geneseo Department of Mathematics

Variations on Integration by Substitution

Friday, November 22

Math 221 06
Fall 2019
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

Review session on Study Day, 12:00 - 1:00, South 328

No SI Monday (Nov. 25)

Questions?

Is the integral of a product equal to the product of the integrals?

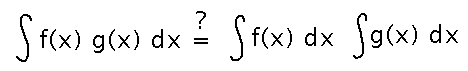
Integral of f times g equals-question integral of f times integral of g

The gold standard in math for answering questions such as this is to have a proof. But there are other ways to at least start to get a sense, for instance to try the idea on an example. And if the example shows that the idea doesn’t hold, then it becomes a “counterexample” that proves the original idea false.

For instance, let’s try the possible equality between integrals of products and products of integrals on 2 simple functions whose product is easy to calculate:

Integrating x times 2 x and multiplying integrals of x and 2 x gives different results

Since the two ways of integrating produce clearly different results, it looks like integrals of products cannot be calculated by finding the product of two separate integrals.

To further confirm that, look at how sums of products and products of sums behave (which is relevant since definite integrals are Riemann sums):

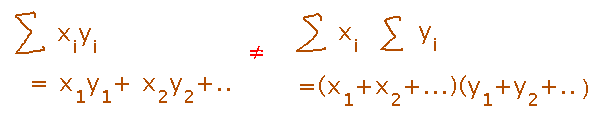
Sum of x times y expands differently from sum of x times sum of y

Once again, the two ways of thinking about sum and product will generally have different values.

Similar thinking can be used in the problem set question about proving the sum rule for integrals, except that there you expect things to turn out equal. So the formal reasoning about sums is going to be most important, perhaps with an example to confirm it, whereas above it was the (counter)example that was most compelling and the formal reasoning was confirmation.

In that problem set question, you can recognize that the Riemann sum form of an integral “hides” the a and b bounds in things like Δx and the calculation of x_i, and so drop explicit mention of a and b while working with sums and bring them back when switching back to integrals (in a completely rigorous proof it would be better to spell out Δx and x_i in enough detail that a and b stay explicitly part of the equations throughout).

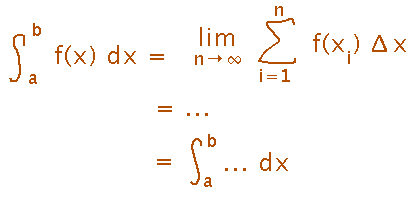
Integral from a to b becomes limit of sum with no a or b

Integration by Substitution

Find the antiderivatives of sin(3x) / cos²(3x)

Start with the substitution u = 3x:

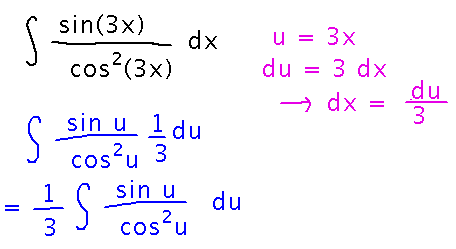
Start integrating sine of 3 x over cosine squared of 3 x by substitution u equals 3 x

This leaves you with a slightly simpler integral, but still not one with an obvious antiderivative. So try substitution again:

Integrate next sine of u over cosine squared of u via substitution v equals cosine u

Moral: sometimes it’s easiest to use a series of substitutions. (Though whenever you do this you could also do it all at once as a single big substitution.)

Find the antiderivatives of x(x+2)⁷. See example 5.33 as a model.

The “obvious” substitution to start with is u = x + 2, except that doing so leaves you with “x” lying around neither included in u nor du. But you can still write x in terms of u, namely x = u - 2. Doing that finishes the substitution:

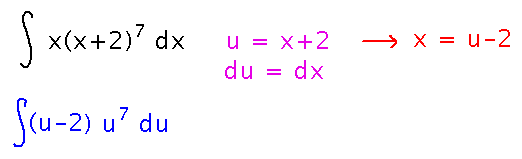
Integral of x times x plus 2 to the seventh becomes integral of u minus 2 times u to the seventh

Substitution in definite integrals.

Read “Substitution for Definite Integrals” in section 5.5.

Next Lecture