SUNY Geneseo Department of Mathematics

The Fundamental Theorem of Calculus, Part 2

Monday, November 18

Math 221 06
Fall 2019
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

SI today: 6:00 - 7:30, Fraser 104.

Questions?

The Fundamental Theorem of Calculus, Part 2

“Fundamental Theorem of Calculus Part 2: The Evaluation Theorem” in section 5.3

Key Idea(s)

In words: if F is an antiderivative of f, then the integral of f from a to b is F(b) - F(a)

Or, in mathematical symbols:

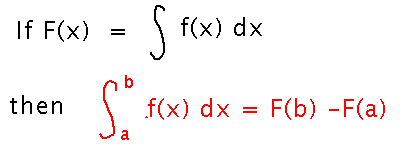
Integral of f from a to b is antiderivative at b minus antiderivative at a

Example

Based on Example 5.20.

Evaluate the integral from -1 to 1 of t3 + 1.

Start by finding an antiderivative of t3 + 1, then plug the bounds of integration into that antiderivative:

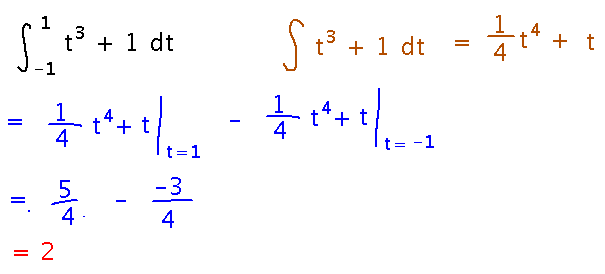
Antiderivative is t to the fourth over 4 plus t, evaluate at 1 and negative 1 and subtract

Using Other Antiderivatives

Evaluate the integral from 1 to e of 1/x.

As before, find an antiderivative and plug in the bounds:

Antiderivative is natural log x, evaluating at e and 1 yields 1 and 0 for integral equals 1

Side note: if you want to use Mathematica to find an antiderivative, you can do it with Integrate, specifying just the variable, not the variable and bounds, as the second argument. For example,...

Example of Mathematica Integrate function

How about the integral from 0 to π/2 of 3(sin x + cos x)?

Use the same process as before, combined with some integration rules to make things simpler (e.g., removing the constant multiple from the integral), and remembering how sine and cosine behave.

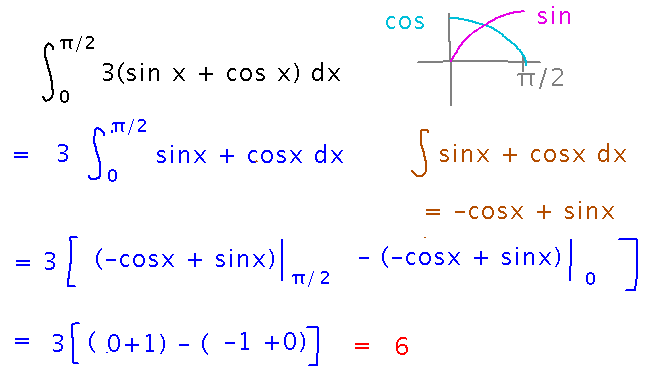
Remove 3 from integral, find antiderivative of sine plus cosine, evaluate at 0 and pi over 2

Applications

The Mathematical Gardeners Club of Geneseo has laid out a flower bed bordered by the x axis and the curves y = (x+1)2 and y = (x-1)2. What is the area of the flower bed (distances measured in yards).

Roughly triangular flowerbed with straight bottom and curved sides

The area in question is the sum of 2 integrals, one for the left side and one for the right. Initially call the left and right bounds a and b, then figure them out later.

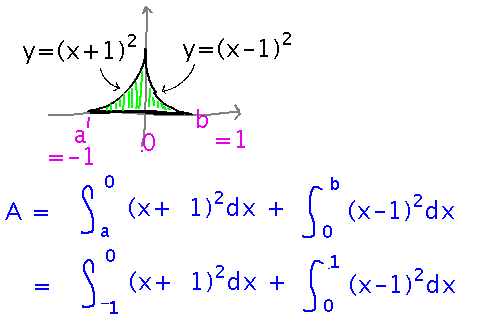
Integral from a to 0 of x plus 1 squared plus integral from 0 to b of x minus 1 squared

Now multiply out the (x+1)2 and (x-1)2 and integrate as before. We’ll do this quickly at the start of class Wednesday.

Problem Set

On many aspects of integrals.

See handout for details.

Next

We can only evaluate integrals of a few functions we know antiderivatives of. For example, we couldn’t directly integrate (x+1)2 and (x-1)2 from the garden example, even though it seems those ought to be easy adaptations of the power rule. We need some more powerful methods....

Integration by substitution.

Read the first part of section 5.5 (up to, but not including, “Substitution for Definite Integrals”).

Next Lecture