The Fundamental Theorem of Calculus, Part 1

Return to Course Outline

Previous Lecture

Misc

Colloquium

“A Concise History of Calculus”

Professors Gary Towsley and Jeff Johannes

Wednesday, November 20, 2:30 - 3:45, Newton 202.

Extra credit for going and writing a paragraph reflecting on connections you make to the talk.

Mid-Semester Feedback

Thumbs up/down

• Needs to make more distinctions between “talk about it” and “more time”
• Needs to allow “talk (for whatever reason)”

More direct instruction

Less harsh grading

Better alignment between instruction and test/problem set questions; chances to practice word problems of the sort that appear on tests.

Questions?

The Fundamental Theorem of Calculus, Part 1

First part of section 5.3 in the textbook.

Key Idea(s)

General idea, albeit lacking a bit of mathematical precision: if F(x) is defined as an integral from anything to x, then F’ is the integrand.

Big over-arching moral, emphasizing the informal idea over mathematical nuance: derivatives and integrals are inverses of each other.

The Basic Idea

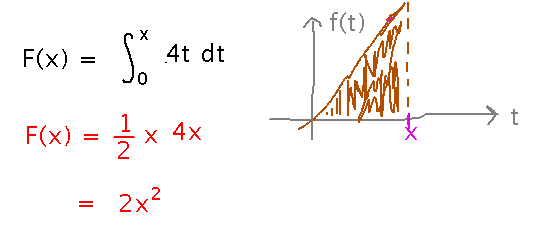
Suppose F(x) is as defined by the Fundamental Theorem, for f(t) = 4t.

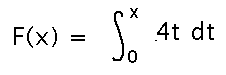
Write F(x) without an integral sign.

The key thing is to recognize that the integral is over a range of t values, x provides the upper end of that range. f(t) is a straight line, the area under it is a triangle, and so the integral can be evaluated using the area formula for a triangle:

Verify that F’(x) = f(x) = 4x. This just takes a quick use of the power rule.

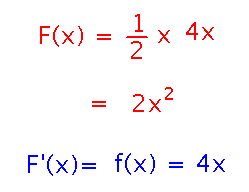
Connecting Integrals and Derivatives

(Based on Example 5.17). If g(x) is the integral from 1 to x of 1 / (t²-1), what’s g’(x)?

Using the Fundamental Theorem immediately gives 1 / (x²-1):

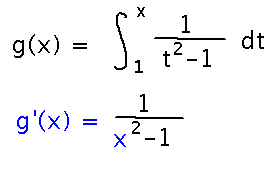
A place this style of function shows up in the real world: probability. Suppose you’re picking a random real number. Since there are an infinite number of reals, the probability of picking any particular one is 0. The interesting questions to ask can’t be “what is the probability of such-and-such a number coming up,” but instead are “what is the probability that the number is in such-and-such a range.” Mathematicians formalize this by defining so-called continuous probability as an integral, with the main idea being that integrating from a to b gives the probability that a number is in the range a to b. Of particular interest are probabilities that the number is less than or equal to some bound, which are integrals from -∞ to the bound. For example, for “bell curve” (formally, “normal”) distributions, the probability that a random number is less than or equal to x is...

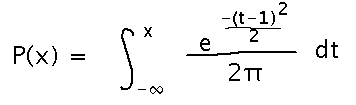
In other words, here’s a function defined in the style of the Fundamental Theorem. Derivatives of those integrals are also interesting, in many ways they act analogously to probabilities of specific events in discrete probability. And they’re easy to calculate, thanks to the Fundamental Theorem.

Next

The Fundamental Theorem, Part 2 (applying the Fundamental Theorem to integrals).

Read “Fundamental Theorem of Calculus, Part 2: The Evaluation Theorem” in section 5.3.

Next Lecture