Introduction to Integration by Substitution

Questions?

Garden Area

The Mathematical Gardeners Club of Geneseo has laid out a flower bed bordered by the x axis and the curves y = (x+1)² and y = (x-1)². The area of the flower bed is the sum of 2 integrals, one for the left side and one for the right. Initially call the left and right bounds a and b, then figure them out later.

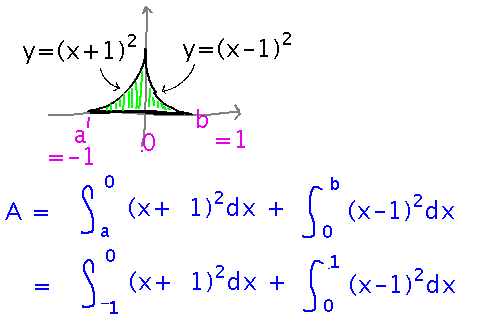
Now multiply out the (x+1)² and (x-1)² and integrate. Both integrals proceed almost identically:

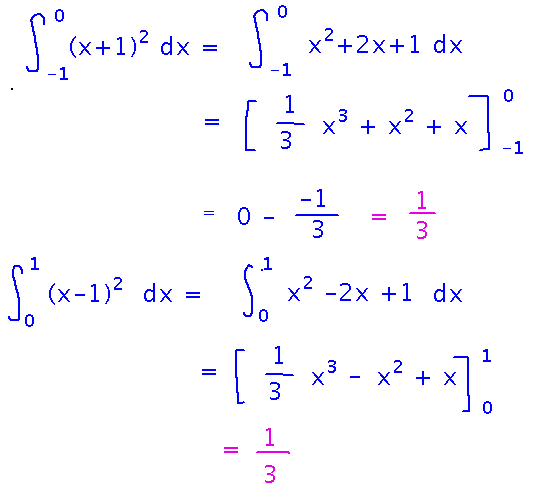
Substitution

Section 5.5, especially re substitution and indefinite integrals (aka antiderivatives).

Key Idea(s)

Procedure: How to use substitution to integrate g(x) dx, at least for the kinds of example we’ve seen so far. A more general version will come soon.

1. (first approximation) Identify u such that g(x) dx = uⁿ du
2. Use the power rule for antiderivatives to find the antiderivatives of uⁿ du

Theory: Substitution is the antiderivative rule corresponding to the chain rule for derivatives.

Example

Based on Example 5.30.

Find the antiderivatives of 8x³(2x⁴-1)³.

Picking u = 2x⁴-1, what looks like an inner function, works well, because everything outside of (2x⁴-1)³ then turns out to be the derivative of u.

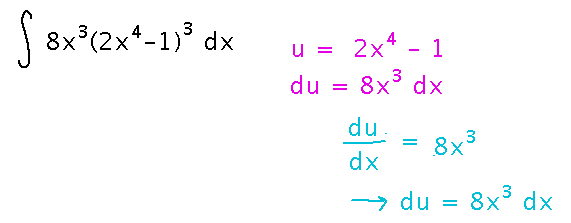
Once you write the integral in terms of u, the rest is just the power rule:

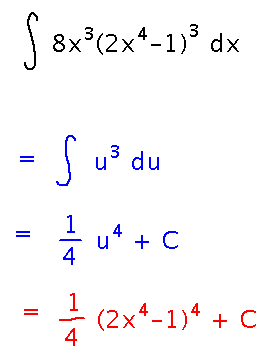
Application to the Garden

Use substitution to find an antiderivative of (x+1)².

You can do this with a substitution in which du is just dx (sometimes this happens):

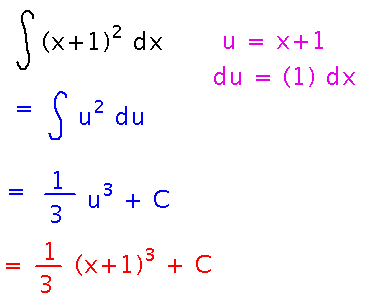
Compare to the antiderivative from multiplying out (x+1)² and then integrating.

At first glance they look different. But the difference is all in the constants of integration, and since either of them can represent any constant, there really isn’t a difference after all.

Next

Practice with more sophisticated substitutions.