SUNY Geneseo Department of Mathematics

Summations and Areas

Friday, November 8

Math 221 06
Fall 2019
Prof. Doug Baldwin

Questions?

Cylinder-in-Sphere

How to set up the cylinder-in-sphere problem in problem set 10?

Scenario is a cylinder of unknown radius and height, that must fit into a sphere of radius 1. This imposes constraints on radius and height.

The formula for the volume of a cylinder gives you an objective function to maximize.

Now think about coming up with equations for the constraints. The key observation is that the corners of the cylinder touch the sphere, so those corners are distance 1 (the sphere’s radius) from the center. Then the lines from the center to the corner of the cylinder, the corner to the cylinder’s axis, and along the axis form a right triangle that provides the constraint:

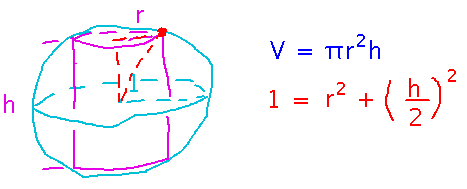
Cylinder inscribed in sphere creates constraint relating cylinder height and radius and sphere radius

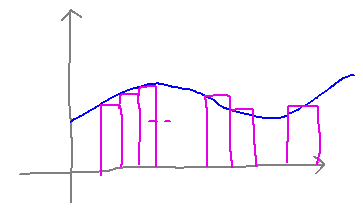
Lower and Upper Sums

What are these ideas from the reading?

When you approximate the area under a graph as a sum of areas of rectangles, you could pick rectangles to consistently stick above the graph, or to consistently lie below (or to not consistently do either). In the first case the area of the rectangles is an upper bound on the area under the graph, i.e., an “upper sum.” In the second case, the rectangles give a lower bound on the area under the graph, a “lower sum.”

Graph with rectangles mostly below, but some stick above and others below

Sums and Areas

Latter part of section 5.1, start of 5.2

Key Idea(s)

Riemann sum (sum of function values times rectangle widths) as an estimate of the area under a graph.

Approximate Area

Based on Example 5.4.

Estimate the area under the graph of y = x²/2 between x = 0 and x = 3 using 6 intervals.

Each rectangle is half a unit wide. Making the right sides of the rectangles touch the graph gives us heights, then just multiply height times width and add up the results:

Graph with area below divided into 6 rectangles, sum of their areas

In summation notation, this is a typical Riemann sum:

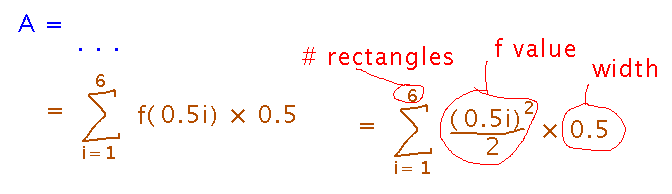
Sigma form, sum from 1 to 6 of function value times width

How about 600 intervals? Use the same idea, except the bound on the summation and the width of the rectangles will be different. And don’t try to evaluate and add up all the areas by hand, use the ideas from yesterday to simplify the sum into a closed form first.

Problem Set

See handout for details.

Riemann sums and definite integrals.

Remainder of section 5.2

Next Lecture