Definite Integrals as Sums

Return to Course Outline

Previous Lecture

Misc

SI session this evening, 6:00 - 7:30, Fraser 104.

Questions?

Definite Integrals

Section 5.2.

Key Idea(s)

The definite integral is the limit of a Riemann sum as the number of intervals goes to infinity, i.e., the same sum as computes the area under a graph.

Picking Up from Friday

We developed a Riemann sum to estimate the area under the curve y = x² from x = 0 to x =3, and estimated it to be 5.6875 square units.

Now, based on example 5.7, see if you can extend that and evaluate the integral of x² from 0 to 3 as a limit of a Riemann sum.

Start by sketching the function and rectangles for a Riemann sum, identify some of the pieces from Friday:

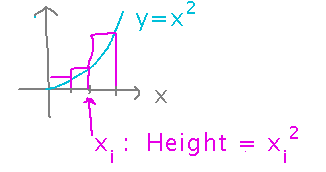
Now fill in a more detailed description, matching the first few steps of the example (namely identifying the width of the intervals, where the x_i are, etc.

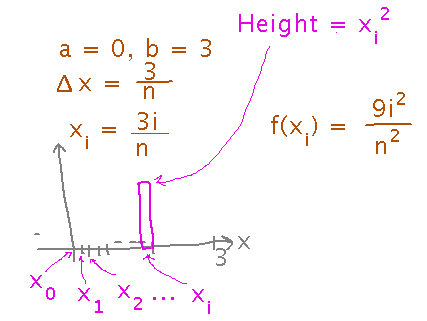
Then, still following the example, write down and simplify the Riemann sum:

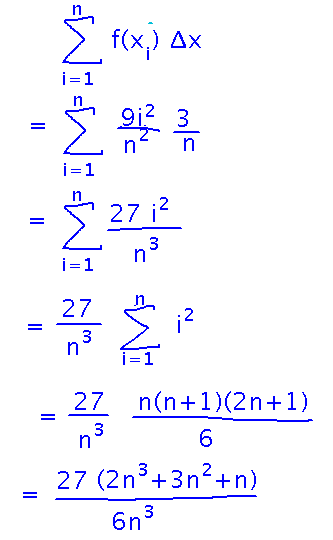
Finally, find the integral’s value by taking the limit of the sum as n goes to infinity. Techniques we recently saw for finding limits at infinity are useful here.

Next

Evaluating integrals as Riemann sums is a pain; there must be a better way

Start looking at using algebraic properties of integrals to make them easier to evaluate.

Read “Properties of the Definite Integral” in section 5.2.

Next Lecture