Summations

Return to Course Outline

Previous Lecture

Misc

SI session this afternoon: 3:00 - 4:30, Fraser 104.

Questions?

Problem set 10 question about finding both a minimum and a maximum for a single function?

Start by finding critical point(s). In this case there’s only one, call it x. Then evaluate f(x), let’s suppose it turns out to be 50. How do you know if that’s a minimum or a maximum?

You still have endpoints to check, and the values there can be compared to this 50. In this problem, you’re looking for positive integers that sum to 10, so one endpoint is 1 (the smallest positive integer) and the other is 9 (the largest integer you can add 1 or more to and still get 10).

Sums and Area Under a Graph

Section 5.1.

Key Idea(s)

Sigma notation: a notation for sums, e.g., 2 + 4 + 6 + 8 + 10. The notation describes a pattern shared by the numbers being added, and bounds on the values to include in the sum.

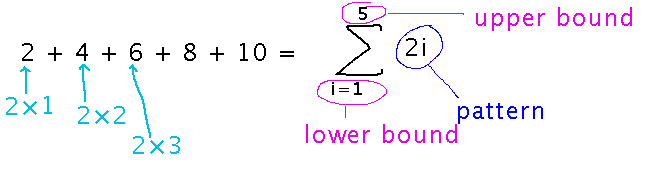
There are algebraic and closed form rules for summations.

Summations will be closely connected to finding areas under curves.

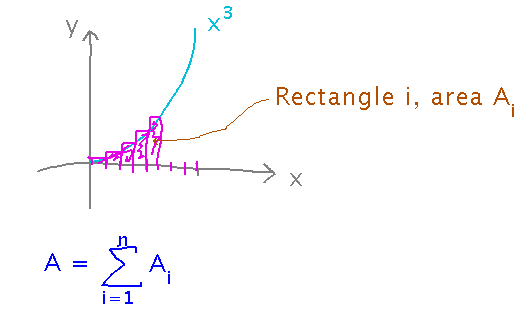
Notation

Based on Example 5.1. Use sigma notation to write the sum of terms of the form 3i for i = 1, 2, 3, 4, 5. Then find the value of the sum.

Algebra and Closed Forms

Based on example 5.2. Use properties of sums to find the sum of i³ - i for i = 1, 2, ..., 5. Also calculate the sum by hand and confirm that it equals what the algebraic analysis tells you.

Start by using algebra and closed form rules to find a closed form for the whole sum. This one assumes n is the generic upper bound:

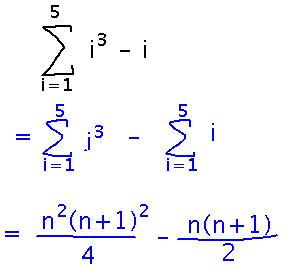
Then plug in the actual value for the upper bound to get a specific numeric answer:

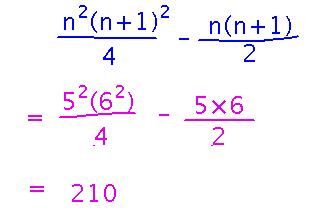
Can you use the closed form rules if the lower bound isn’t 1? No, but you can rewrite sums with other lower bounds as differences of sums that start at one, using one of the algebraic rules. For example...

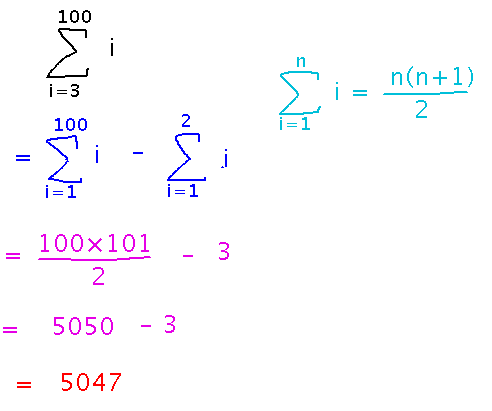
Next

Areas under graphs and definite integrals.

Read section 5.2.

Next Lecture