SUNY Geneseo Department of Mathematics
Friday, November 1
Math 221 06
Fall 2019
Prof. Doug Baldwin
No more Sunday hours.
All other hours stay the same (roughly, mid-day and evening, Monday through Friday).
Hour exam 2 is Monday (November 4).
Covers material up through problem set 8 that wasn’t covered on the first hour exam, i.e., problem sets 6 through 8. Topics include, for example, the chain rule; implicit differentiation; derivatives of exponential, logarithmic, and inverse functions including inverse trig; related rates; extreme values; Mean Value Theorem.
Rules and format similar to first hour exam, especially open-references-closed-person rule.
Sample questions are available in Canvas.
No SI session Monday.
When I mow the lawn, I somehow manage to end up with the lawn mower diagonally opposite the shed it lives in. The lawn is roughly 300 feet by 100 feet, and I can push the lawn mower at a speed of 4 feet/second on the grass or 12 feet/second on the driveway.
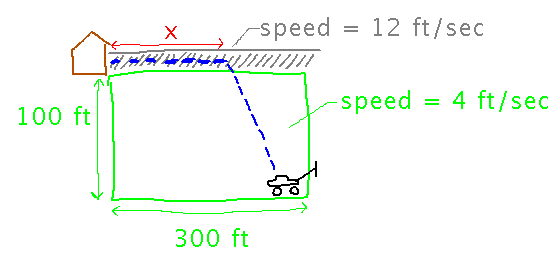
What place on the driveway (i.e., value of x) should I head for in order to minimize time to the shed?
Start by finding equations for relevant quantities (e.g., time).
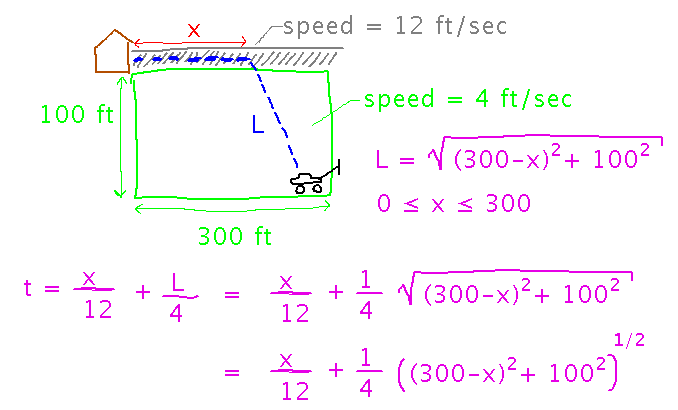
Once you have the quantity to optimize (time in this example) expressed in terms of one other variable (x in this example), take the derivative and simplify if appropriate:
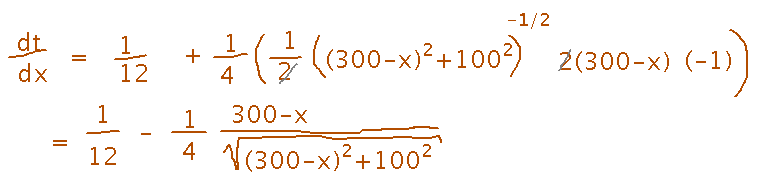
Finally, solve for the value(s) of x that makes the derivative 0.
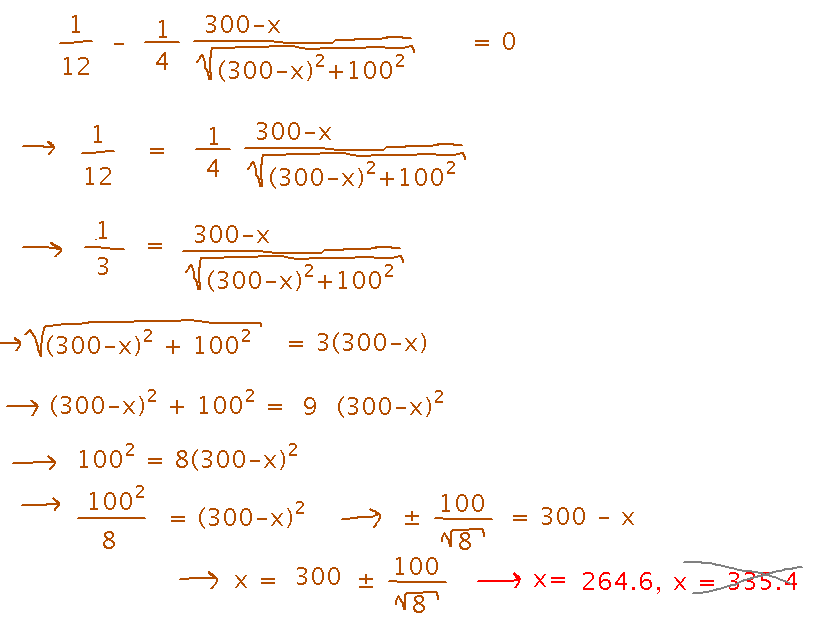
Notice that we had 2 solutions, but one of them violates an implicit constraint from the problem, namely that x has to be a distance that actually lies on the driveway, so in particular no bigger than 300 feet.
The last step is to make sure that setting x to one of the endpoints of its possible range (0 and 300 in this case) doesn’t give a better optimum. So for x values of 0, 265 (roughly the value we found), and 300, the times are
So cutting diagonally across the lawn to the point on the driveway 265 feet from the shed does indeed give me my minimum time.
(After the exam)
L’Hospital’s rule.
Read section 4.8.