Misc
Exam 2
Hour exam 2 is next Monday (November 4).
Covers material up through problem set 8 that wasn’t covered on the first hour exam, i.e., problem sets 6 through 8. Topics include, for example, the chain rule; implicit differentiation; derivatives of exponential, logarithmic, and inverse functions including inverse trig; related rates; extreme values; Mean Value Theorem.
Rules and format similar to first hour exam, especially open-references-closed-person rule.
Extended SI session Thursday, 5:00 - 8:00, Fraser 104.
Sample questions are available in Canvas.
Questions?
Mt Doom ski hill, part C (where is the steepest slope)?
The slope of the hill is the derivative of elevation, h’(x)
So the steepest slope is the maximum value of h’(x) over [0,π]
Solve this like other maximum value problems: find critical points, compare h’(c) for each critical point c to h’(0) and h’(π) to find the largest.
What about finding the corresponding angle? Normally you think of slope, m, as change in y over change in x. But if you fix change in x at 1, then change in y must be m, and suddenly you have a right triangle with sides of length m and 1 opposite and adjacent, respectively, to the angle used as the angle of incline:
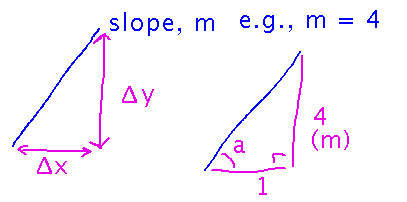
This means the slope is also the tangent of that angle, so the angle can be found as the inverse tangent of slope:
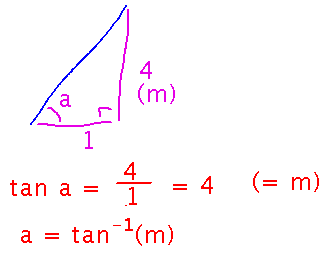
Optimization Examples
Optimal Bucket
You would think that companies that make buckets would want to minimize the amount of plastic they need to make a bucket of a certain volume, which is equivalent to minimizing the surface area of the bucket. Do they really do this?
What is the minimum surface area of a cylindrical bucket that holds 3 gallons (= 693 cubic inches)?

Start by expressing h and A solely in terms of r:
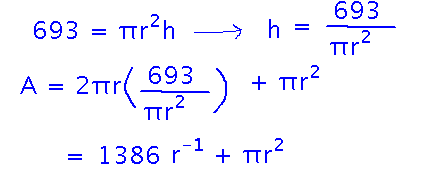
Then find value(s) of r at which the derivative of A is 0:
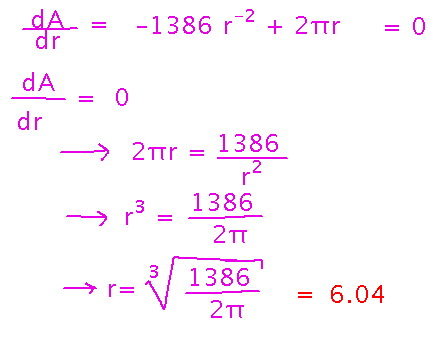
How do we know this gives minimum surface area as opposed to maximum? If the possible values for r were in a closed interval we’d check the endpoints, and see if they produced larger or small surface areas. Here r can be any value greater than 0, so there isn’t a closed interval. But since r can be arbitrarily close to 0, and arbitrarily large, we can use limits to see what happens to area as r approaches the extremes of its possible values:
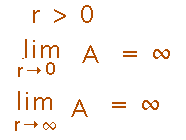
We haven’t calculated area when r = 6.04, but it will be finite, which is less than the extreme values. So we did indeed find the radius that provides minimal surface area, and thus minimal plastic to make the bucket.
Lawn Mowing
When I mow my lawn, I somehow always end up in the corner farthest from the shed the lawnmower lives in. There’s a driveway along one side of the lawn, leading to the shed. I can push the lawnmower at a speed of 12 feet per second on the driveway, and 4 feet per second on the grass. What point on the driveway should I head for in order to minimize time to the shed?
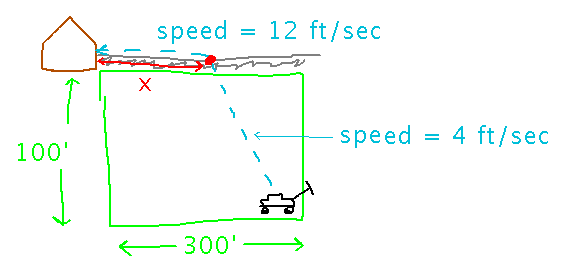
Think about this for tomorrow. We’ll discuss/develop solutions then.
Next
More optimization examples.