L’Hospital’s Rule

Return to Course Outline

Previous Lecture

Misc

PRISM bowling this Friday.

Problem set. See handout for details.

Questions?

Limits at infinity for ratios? A general process is…

1. Factor and cancel high-order term in denominator
2. Remaining terms of the form 1/xⁿ go to 0
3. Other terms are either constant or infinite by limit laws

For example:

(And notice that such problems can often also be solved using L’Hospital’s rule too.)

L’Hospital’s Rule

Section 4.8.

Key Idea(s)

A way to find limits that are indeterminate for either of 2 reasons (and other indeterminate forms can sometimes be rewritten into one of these):

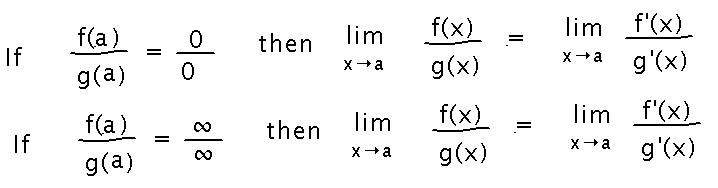
Example

Based on Example 4.38. Find the limit as x approaches 1 of (1 - x)/cos(πx/2)

Since plugging x = 1 into the function gives 0/0, which is an indeterminate form handleable by L’Hospital’s rule, use it. In other words, differentiate the numerator and denominator, and see if the limit of the ratio of the derivatives is evaluable.

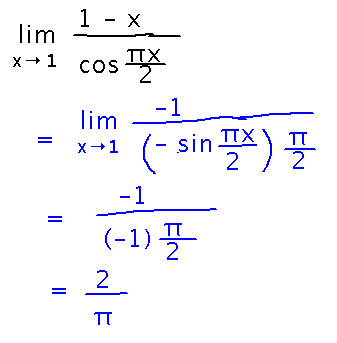
∞/∞ Example

Based on Example 4.39. Find the limit as x approaches infinity of 3x² / (x² + 3).

This time plugging infinity into the function leads to infinity over infinity, the other indeterminate form L’Hospital can handle.

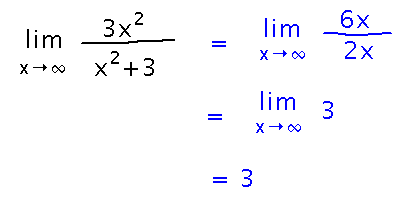
What if the function were 3x² / (x² + 3x). Now x doesn’t cancel out of the derivatives as nicely as it did in the first version of this example, and the limit of the ratio of the derivatives is another indeterminate form. But it’s one that L’Hospital can handle, so use the rule a second time:

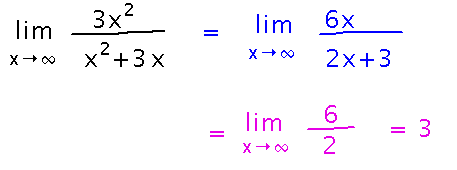
Next

Sums and areas under graphs

Read section 5.1

Next Lecture