General Derivatives of Inverse Functions

Return to Course Outline

Previous Lecture

Misc

Problem set on the chain rule (and derivatives of transcendental functions).

Questions?

I’m hoping to have the tests graded when you get back from break.

The General Power Rule

So far, we’ve been able to prove that the power rule for derivatives works if the power is…

• Any integer
• A fraction of the form 1/b for any non-zero integer b.

But we don’t know for sure that it works for general fractions a/b where a is any integer, b any non-zero integer.

Prove it now.

The key step is to realize that you can break the exponent into two parts, each of which you can use the power rule on:

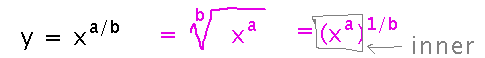
Then you can use the chain rule on the double exponentiation, and simplify:

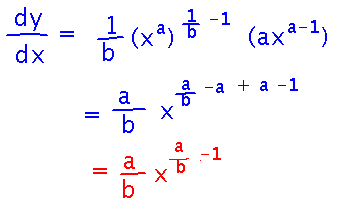
General Derivatives of Inverse Functions

Suppose you know f’(x) for some function f(x), can we work out a general rule for the derivative of f^-1(x)?

Examples

f(x) = e^x, f’(x) = e^x, f^-1(x) = ln x

f(x) = x², f’(x) = 2x, f^-1(x) = √x

f(x) = sin x, f’(x) = cos x, f^-1(x) = sin^-1 x = arcsin x

Beware: the “-1” superscript in this notation does not mean raise to the -1 power, i.e., take the reciprocal! (Even though any other superscript, particularly with a trig function, would mean raising to a power.)

Derivation

Follow the same procedure we did to find derivatives of inverses of specific functions, i.e., rewrite the starting equation in terms of the original function, differentiate both sides with respect to x, isolate the dy/dx term, and simplify to express dy/dx in terms of x:

Next

Concrete examples of using the inverse function theorem.

Then start related rates problems.

Read section 4.1.

Next Lecture