SUNY Geneseo Department of Mathematics

General Derivatives of Inverse Functions, Part 2

Thursday, October 10

Math 221 06
Fall 2019
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

SI today, 3:00 - 4:30, Fraser 104.

Questions?

Derivatives of Inverse Functions

Inverse function theorem: If function f(x) has derivative f’(x), then f^-1(x) has derivative 1 / f’(f^-1(x)).

What does this actually mean?

Simple Example

Let f(x) = x², so f’(x) = 2x and f^-1(x) = √x. We already know that the derivative of f^-1 is 1/(2√x).

Listing f, f prime, f inverse, and f inverse prime.

Can you get that same function by applying the inverse function theorem?

Yes, by noticing that f^-1(x) is √x, so applying f’ to that yields 2√x, and finally the reciprocal is 1/(2√x).

1 over 2 root x is 1 over derivative of f applied to inverse of f

Inverse Trigonometric Functions

Use the inverse function theorem to find the derivative of arcsin x aka sin^-1x

Start by cataloging the pieces, to plug into the inverse function theorem.

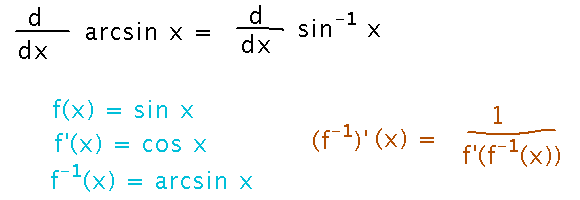
Want derivative of inverse sine so f is sine, f prime is cosine, f inverse is inverse sine

Applying the inverse function theorem to these pieces is easy, but gives a result very different from what the Internet says is the derivative of sin^-1x.

Derivative of inverse sine is 1 over cosine of inverse sine of x

To see that these are actually the same, use the definitions of the trigonometric functions to label the sides of a right triangle in ways that produce an angle whose sine is x, then express the cosine of that angle in terms of the lengths of other sides:

Triangle with hypotenuse 1, sides x and root 1 minus x squared shows cosine of inverse sine x is root 1 minus x squared

This differentiation rule also leads to an antiderivative rule that is sometimes helpful:

Integral of d x over root 1 minus x squared is inverse sine of x

You can similarly find derivatives of the other inverse trigonometric functions. For example, how about arctan aka tan^-1?

Follow the same procedure, i.e., apply the inverse function theorem and then use a triangle to help express the various trig functions involved in terms of x, constants, etc. This time that’s a little trickier than it was for sin^-1, because the functions in question are tangent and secant (secant squared, even), but the basic idea is the same:

Derivative of inverse tangent via inverse function theorem and triangle with sides x and 1

And as before, there’s also an occasionally useful antiderivative rule too:

Integral of d x over 1 plus x squared is inverse tangent of x