SUNY Geneseo Department of Mathematics

Derivatives of Inverse Functions

Friday, October 4

Math 221 06
Fall 2019
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

First hour exam is Monday (October 7) in class.

Covers material from problem sets 1 through 5.

You’ll have the whole class period.

5 short-answer questions, focusing on applying ideas from the course.

Sample questions are now available in Canvas. Beware that question 5 requires the chain rule (which won’t be on the exam) to solve, but also involves trigonometric derivatives (which will be).

Open book, open notes, open computer as a reference/calculator; closed person.

Questions?

Inverse Functions

Motivation: we now know how to differentiate a lot of functions without knowing how to differentiate their inverses. For example, ex but not ln x, sin x but not sin-1x (aka arcsin x), even x2 but not √x.

But implicit differentiation gives us a way to fix this.

Example

Suppose y = ln x. Can you rewrite that equation into something that only involves functions you know how to differentiate, and then use implicit differentiation to find dy/dx?

Start by raising e to both sides of the equation, to get rid of the logarithm:

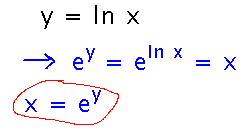
Rewrite y equals ln x as x equals e to the y

Then do implicit differentiation, much as we did yesterday:

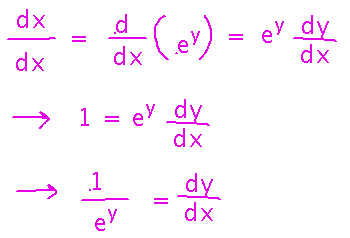
Differentiate both sides of equation and simplify

Finally, express the result in terms of x (the original variable of interest). Now we have a new differentiation rule, namely for natural logarithms:

1 over e to the y becomes 1 over x

This also implies a new anti-derivative rule, which turns out to be surprisingly useful:

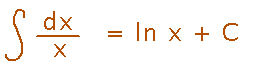
Antiderivative of 1 over x equals ln x plus C

Another Example

Suppose y = √x; find dy/dx.

Do this much as we did above, namely rewrite the original equation in terms we can differentiate, use implicit differentiation, and express result in terms of x:

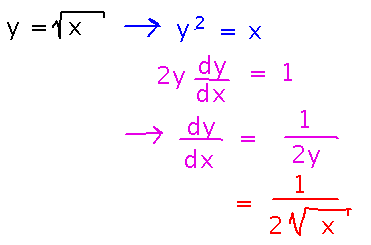
y equals root x implies x equals y squared, differentiating yields d y over d x equals 1 over 2 root x

Oddly, this is exactly what we’d get if the power rule for derivatives worked on fractions:

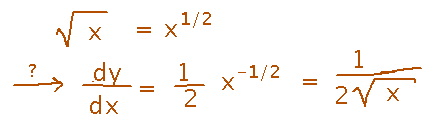
Power rule applied to x to the 1 half yields 1 over 2 root x

So maybe it does, Let’s see if we can prove it...

Generalizing the Power Rule

If y = x1/n, what is dy/dx?

Proof power rule for exponents of the form 1 over n via implicit differentiation

So the power rule does work for fractions of the form 1/n!

Next

(After the exam)

Finish proving the power rule for fractions of the form a/b for integers a and b.

Look at derivatives of inverse trigonometric functions.

Prove a general derivative-of-inverse-function rule.

Next Lecture