Misc
SI Session
3-hour session today.
5:00 - 8:00, Welles 131.
No SI Monday.
First Hour Exam
Next Monday, October 7, in class.
Covers material from problem sets 1 through 5 (i.e., the problem sets that will have been graded by the day of the exam).
You’ll have the whole class period.
Probably 3 to 5 short-answer questions, focusing on applying ideas from the course.
Sample questions are now available in Canvas. Beware that question 5 requires the chain rule (which won’t be on the exam) to solve, but also involves trigonometric derivatives (which will be).
Open book, open notes, open computer as a reference/calculator; closed person.
Questions?
Implicit Differentiation
Section 3.8
Key Idea(s)
To differentiate an implicit equation wrt x
- Differentiate both sides wrt x…
- …using chain rule whenever there’s a variable other than x
- Use algebra to isolate derivative
Examples
Suppose x2 - y2 = 1. What is dy/dx? Does it even make sense to ask?
It does make sense to ask. Even though this equation doesn’t define a function, it does define a curve for which it is reasonable to talk about rate of change, i.e., how fast y values along small segments of the curve change as x values change.
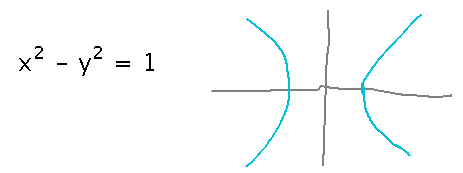
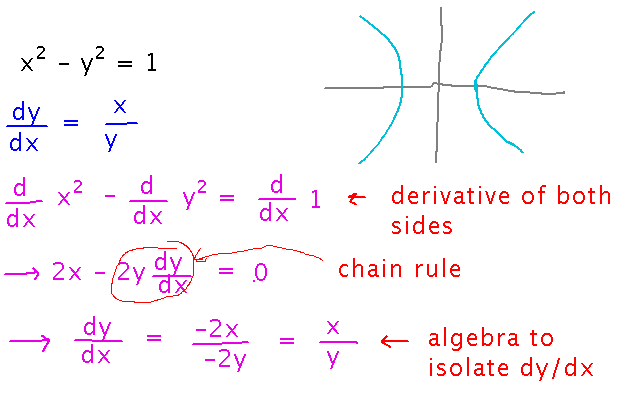
What is dy/dx?
Here’s how the strategy outlined under the “key idea” above answers this:
As a step towards applying implicit differentiation to inverse functions, consider x = y2, and consider finding dy/dx (i.e., not the derivative suggested by reading the equation as an explicit definition of x):
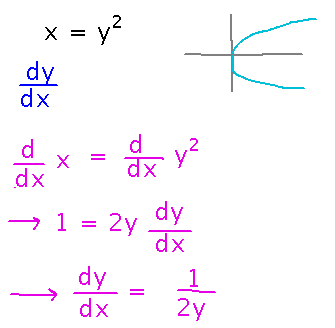
Another thing we’ll want to do when working with inverse functions is use implicit differentiation, but then at the end express one variable in terms of another. For example, here’s an implicit equation and a derivative...
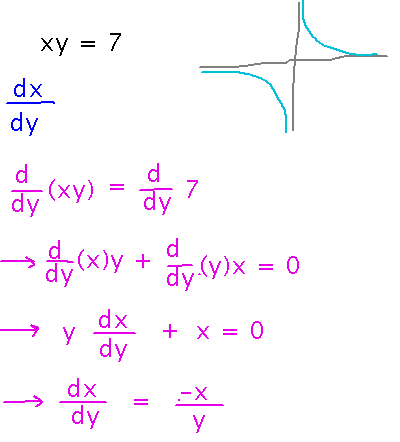
But this derivative can also be found by rewriting the equation into explicit form and using the quotient rule:
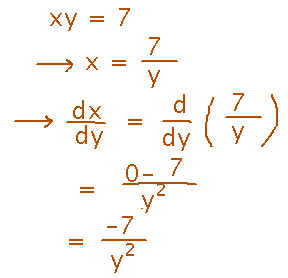
The result looks very different from what we got with implicit differentiation, until you realize that variable x in the result from implicit differentiation is expressible in terms of y:
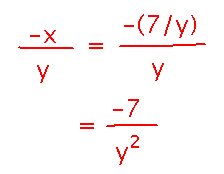
Next
Implicit differentiation and inverse functions.
No reading!