Derivatives of Exponential Functions

Return to Course Outline

Previous Lecture

Misc

SI Session

3-hour session tomorrow (Thursday).

5:00 - 8:00, Welles 131.

No SI Monday.

First Hour Exam

Next Monday, October 7, in class.

Covers material from problem sets 1 through 5 (i.e., the problem sets that will have been graded by the day of the exam).

You’ll have the whole class period.

Probably 3 to 5 short-answer questions, focusing on applying ideas from the course.

I’ll make some sample questions available.

Open book, open notes, open computer as a reference/calculator; closed person.

Questions?

Exponential Functions and Their Derivatives

“Derivative of the Exponential Function” in section 3.9

Key Idea(s)

Derivative of e^x is e^x.

Derivative of c^x is (ln c) c^x. (This wasn’t in the reading for today, we worked it out ourselves.)

An interesting idea, although not really “key”: book defines e as the number such that if function b(x) = e^x, then b’(0) = 1.

Examples

Find the derivative of e^x + 1

Take derivatives of both terms in the sum, using the differentiation rule for e^x:

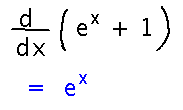
Find s’(t) if s(t) = e^t2-3t

Use the chain rule with the differentiation rule for e^x (they can, like all rules, be used together):

Find the derivative of ue^u.

This time, use the product rule with the rule for e^u:

Antiderivative Rule

The antiderivative of e^x is…

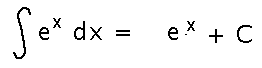
General Exponential Functions

What is the derivative of (e²)^t?

Use the algebraic rule of exponents that (a^b)^c = a^bc. Then use the chain rule:

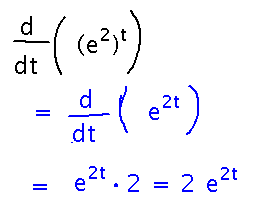
Can you express the number 17 as a power of e? What power? Why?

Yes, 17 = e^{ln 17}, because logarithms and exponentials are inverses of each other.

Def: ln x = the power you raise e to in order to get x. Similarly with logarithms to other bases.

e.g., ln (e²) = 2

log₁₀ 1000 = 3

Useful in solving equations where the variable is in an exponent, e.g., to solve e^x = 7 take logs of both sides, to get x = ln 7.

What is dy/dx if y = 17^x?

Write 17 as e^{ln 17}, then use the same algebra and chain rule we used for (e²)^t:

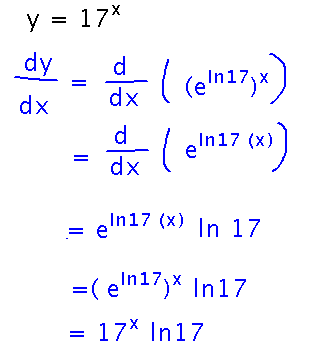
What we did here generalizes, giving a rule for derivatives of exponential functions to any base.

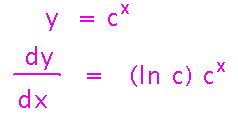
Next

Ultimately, derivatives of logarithms. But they’re easiest to deal with as inverses of exponential functions, via a general way of finding derivatives of inverse functions. And that “general way” comes from something called “implicit differentiation.” So...

Implicit differentiation is next.

Read section 3.8.

Next Lecture