Misc
MLC Review Sessions
Algebra: Thursday (September 19), 6:00 - 7:00 PM, Math Learning Center.
Trigonometry: Next Wednesday (September 25), 6:00-7:00 PM, Math Learning Center.
Math Picnic
This Friday (September 20), 4:30 PM, Highland Park (up Oak St. from campus)
Questions?
Differentiation Rules
First 3 subsections of section 3.3
Key Idea(s)
Rules:
- The derivative of any constant is 0 (constant rule)
- Sum rule
- Difference rule
- Constant multiple rule
- Power rule
Examples
Find the derivatives of...

Derivation
Prove the constant multiple rule (if f(x) = k g(x) then f’(x) = k g’(x)) from the limit definition of derivative.
Start with the limit definition, then plug in the definition of f(x) in terms of k and g(x). Factor k out of the terms inside the limit, then move it outside the limit (thanks to the constant multiple limit law). Now the limit is the definition of g’(x).
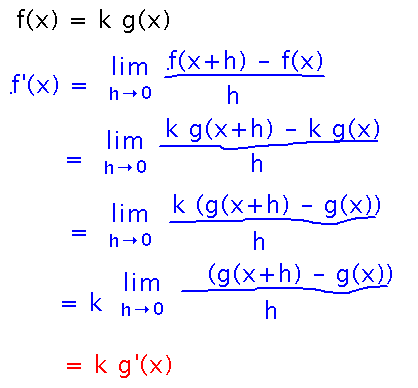
Antiderivatives
You can use differentiation rules to answer questions of the form “what is the derivative of ...?” You can also use them “in reverse” to answer questions of the form “what has ... as its derivative?”
For Example...
What function(s) has 2 as its derivative?
f(x) = 2x, f(x) = 2x + 1, 2x - 3, ... f(x) = 2x + C
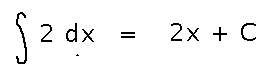
Notice that there are many functions, differing by a constant, since no matter what that constant is, its derivative will be 0.
What function(s) has 4x - 16 as its derivative?

Use the power rule in reverse to figure out what the coefficients and exponents would have to be in order to produce 4x and 16 as derivatives. And notice in doing this that we’re also using the difference rule in reverse.
Problem Set
...on basic derivatives and antiderivatives
See handout for details.
Next
More variations on derivatives, picking up where we left off with antiderivatives.
Read the “Graphing a Derivative” through “Higher Order Derivatives” subsections of section 3.2.
Also bring computers to class to explore derivatives with Mathematica.