Geneseo Math 221 06 Derivative Intro

Misc

SI Session

This evening, 6:00 - 7:30, Fraser 104

REU and Internship Info

Presentations by PRISM students on internship and research experiences — “what can you do with math?”

Thursday, September 19, 5:30 PM

Welles 26

Questions?

How to calculate 1-sided limits with absolute values? The general idea is to use information about what value x is approaching and from which side to determine that the expression inside the absolute value will either always be positive, or always be negative, and thus to simplify away the absolute value operation.

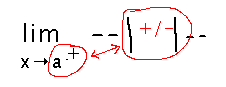
x approaching a from above in limit interacts with absolute value in function

Derivatives

Section 3.1

Key Idea(s)

Formulas for slopes of secant & tangent lines.

Two such formulas, both based on limits.

Slope of a secant line is the average rate of change, slope of tangent is instantaneous rate of change.

Galileo, Again

Back at the beginning of the semester, we used Galileo’s study of falling objects as a motivation for calculus. Galileo could tell that the distance, y, that an object fell in time t was proportional to t², but could only get average speeds.

Assuming y = t², can you now find the exact instantaneous speed of the object at 4 seconds?

Yes, use the slope of the tangent line at t = 4. Use the “( f(t) - f(a) )/ (t - a)” formula:

Factor numerator to get limit as x approaches 4 of f(x) minus f(4) over x minus 4 is 8

How about a general formula for speed in terms of time?

Yes, we can do this now too, using the “( f(a+h) - f(a) ) / h” formula:

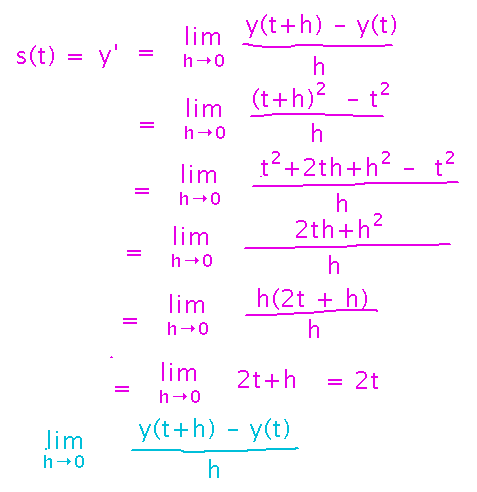
FOIL and cancel to get limit as h approaches 0 of f of t plus h minus f of t all over h is 2t

Example 2

If f(x) = 1/x², what is f’(1)?

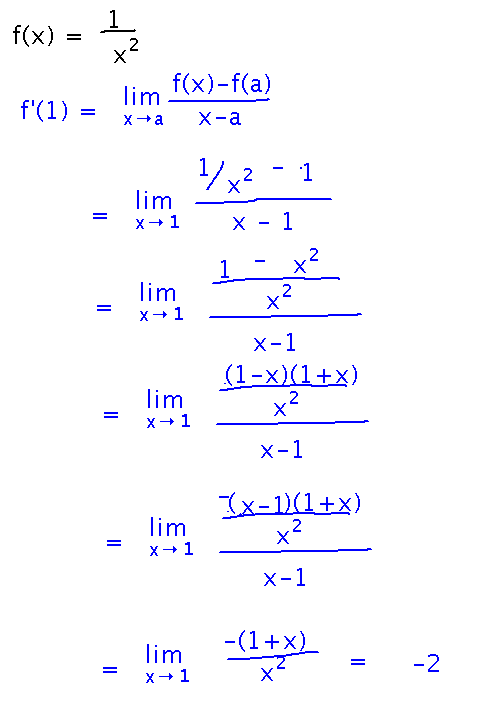
Common denominator and factoring gives limit as x approaches 1 of f of x minus f of 1 all over x minus 1 is -2

Differentiation rules.

Read the “Basic Rules” through “Sum, Difference, and Constant Multiple Rules” subsections of section 3.3 (top of page 247 through first half of page 253).

Derivatives as Limits