SUNY Geneseo Department of Mathematics
Thursday, September 19
Math 221 06
Fall 2019
Prof. Doug Baldwin
SI session this afternoon 3:00 - 4:30, Fraser 104.
“What function has … as its derivative?”
For example, what is the general antiderivative of 3x5 + 2x4 - 6x3 + x2?
We worked this out sort of seat-of-the-pants, although systematically in some ways, e.g., realizing that to get a derivative of the form, say, 3x5, we’d have to start with a power of x higher by 1, and a coefficient that when multiplied by that power would produce 3.
The fact that we had semi-systematic ways of finding this antiderivative suggests we can find general antiderivative rules corresponding to the differentiation rules. We can then use these rules to find antiderivatives:
Use the D function to take a derivative.
Mathematica has its own unique ideas about how to display results. The Simplify function might help rearrange them into forms easier to recognize.
See the demonstration in this notebook.
Derivatives of derivatives.
For example, if y = 2x3 - 6x, what is d2y/dx2? How about the 3rd derivative?
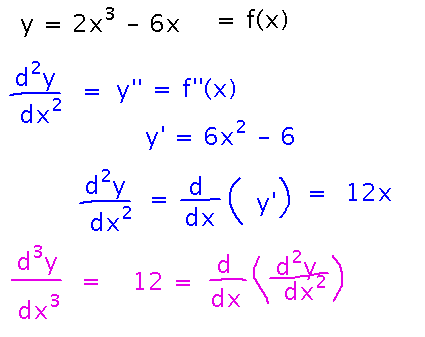
We noticed a pattern in these derivatives, that they were always heading towards a situation where they would become 0. This led to the conjecture that functions of the form xn have n non-0 derivatives.
Look at some examples of non-continuity. In every one, the idea of the slopes of secant lines over ever-smaller intervals (i.e., the limit definition of derivative) breaks down at the discontinuity.
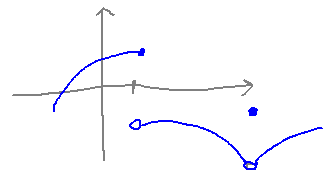
This leads to another conjecture (which is actually the key point of the textbook section on derivatives and continuity), namely that functions don’t have derivatives at discontinuities. Usually stated as having a derivative at a certain point implies continuity at that point.
The product and quotient rules.
Read subsections “The Product Rule,” “The Quotient Rule,” and “Combining Differentiation Rules” in section 3.3.