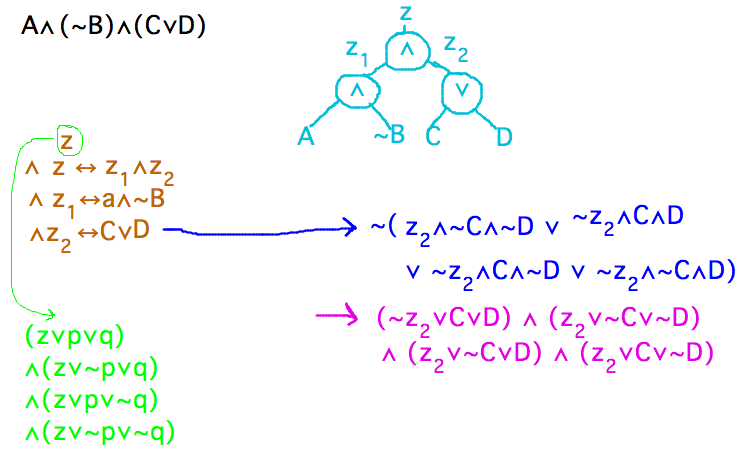
- Multi-step reduction
- Express boolean formula as binary expression tree
- Express tree as conjunction of equivalences (if-and-only-if)
- Rewrite equivalences as complements of DNF expressions
- Negate DNF via de Morgan’s law to get CNF
- Example
- Summary of section 34.5 “The clique problem”
- Clique = subgraph in which all vertices are connected to all others
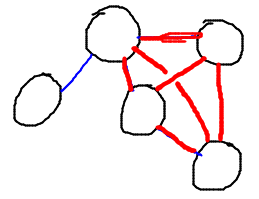
- Problem = does graph G contain clique of size k
- NP completeness proof
- CLIQUE in NP
- Verifier uses candiate clique as certificate, checks edges
- 3-CNF-SAT reduces to CLIQUE
- Construct graph whose vertices represent literals in clauses, and edges
exist between all literals not in same clause and able to be simultaneously true
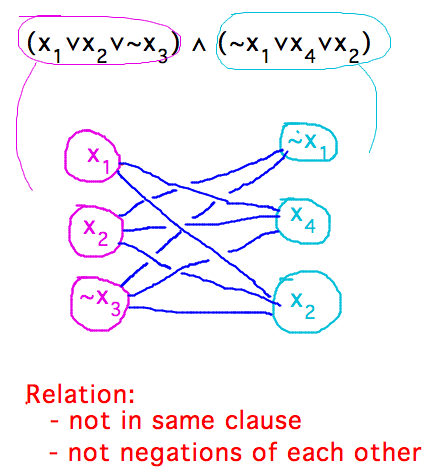
- Construct graph whose vertices represent literals in clauses, and edges
exist between all literals not in same clause and able to be simultaneously true
- CLIQUE in NP
- Clique = subgraph in which all vertices are connected to all others
- More NP completeness examples
- Read rest of section 34.5