- Tell me today if you want to do a presentation
- Colloquium
- “Making Infinity Finite - Zeno’s Paradoxes, Sequences, and Filters”
- John Reynolds, Kansas University (and Geneseo math alum)
- Wednesday, Dec. 2, 2:45
- Newton 204
- Extra credit for write-ups
- (Section 34.5)
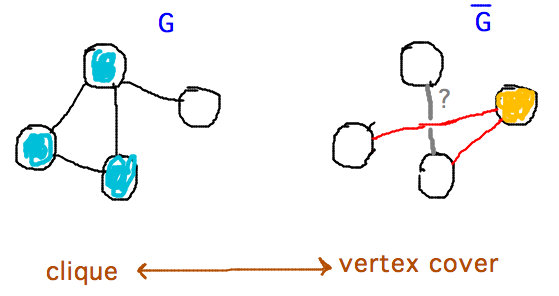
- Vertex cover
- Reduction from clique
- Uses complement of graph
- Vertices (actually edges) not in graph? Complement?
- Complement of G has edges between all pairs of vertices not connected by edges in G and vice versa
- Key idea in proving reduction correct is that every pair of vertices
not in vertex cover of G-complement must be connected by an edge
in G, which makes them a clique
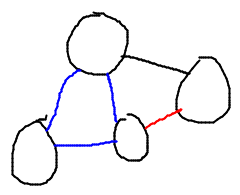
- Example of reduction looking at variant on inputs to problem
- Hamiltonian cycle
- Vertex cover reduces to Hamiltonian cycle
- Show constructed graph has Ham. cycle iff original has vertex cover of size k
- Hamiltonian cycle vs clique?
- Hamiltonian cycle: path of 1 or more edges from each vertex to each other, form cycle
- Clique: one edge from each vertex to each other
- Widget?
- Represents an edge
- Labeled by start vertex, end vertex (even though edges aren’t really directed)
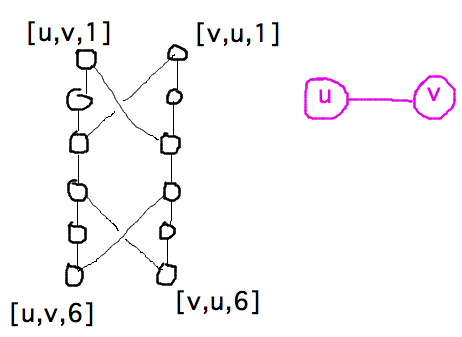
- Reduction constructs one widget per edge
- Plus k selector vertices
- (u,v) sides of widgets connect into chains representing edges incident on each vertex u
- Selectors are “placeholders” that can be “filled in”
to represent any vertex, and so are connected to start and end of each chain

- Example of reduction building “machine” to solve problem
- Traveling salesperson
- Subset sum