- Problem set graph isomorphism question—use a reduction?
- Probably not, this problem set doesn’t need you to do reductions
- Summary of section 34.4
- Formula satisfiability instead of circuit satisfiability
- Boolean variables connected with logic operations
- Formula satisfiability proved NP complete
- CIRCUIT-SAT ≤p SAT means what about relative complexities?
- Really only that CIRCUIT-SAT is no more than polynomially more complex than SAT
- Particular reduction tells you something about the polynomial in “polynomially more,” but not that there isn’t a smaller polynomial in a cleverer reduction
- 3-CNF-SAT
- Conjunctive normal form = formula is conjunction of disjunctions
- 3-literal clauses combined by and
- Also NP complete
- Conjunctive normal form = formula is conjunction of disjunctions
- NP-hard vs NP-complete?
- NP-complete = everything in NP reduces to it, and in NP
- NP-hard = everything in NP reduces to it, not necessarily in NP itself
- Formula satisfiability instead of circuit satisfiability
- Are there things not in NP and if so what?
- Problems in co-NP (maybe)
- e.g., complement of partition problem, i.e., is there no way to partition a set of numbers into 2 subsets with the same sum
- Extensions of SAT (maybe)
- Think of SAT as having a quantifier: do there exist x1, x2, …, xn st Φ(x1,x2,…,xn) = true
- You could add more quantifiers
- For example, do there exist x1, x2, …, xn st for all y1,…,ym Φ(x1,x2,…xn,y1…,ym) = true
- Limit of this process of adding quantifiers is “quantified
boolean formulas” which is PSPACE complete
- PSPACE = problems that require polynomial memory
- Problems in co-NP (maybe)
- Example: construct 3-CNF formula from circuit
- Part 1: circuit to formula reduction
- You can’t just substitute formulas for gate inputs into formulas for gates, because fan-out might grow exponentially
- So construct formulas for values on wires

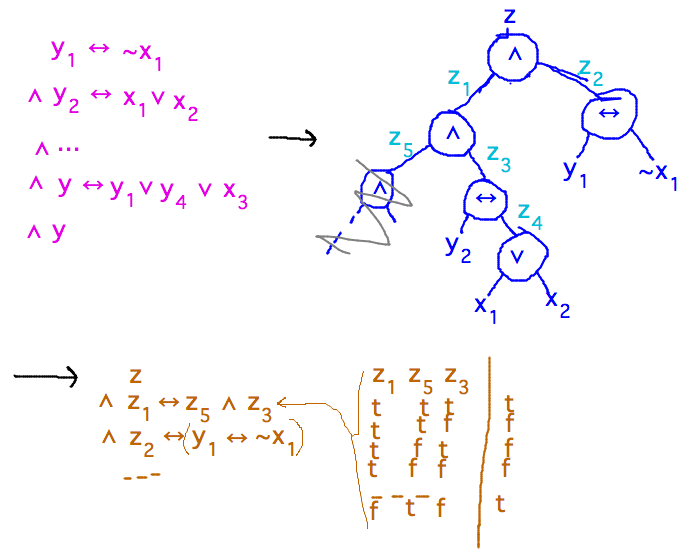
- Part 2: general formula to 3-CNF formula reduction
- Express formula as a tree of binary boolean operations; label edges in tree with new variables
- This gives formula as a conjunction of clauses with at most 3 literals in each
- But those clauses aren’t necessarily disjunctions
- Part 1: circuit to formula reduction
- Finish exploring reduction from formula to 3-CNF
- Then NP completeness in a wider variety of contexts
- Read section 34.5 re clique (first subsection)