SUNY Geneseo Department of Mathematics
Wednesday, May 8
Math 239 01
Spring 2019
Prof. Doug Baldwin
9:00 AM to 3:30 PM weekdays through Wednesday of finals (added 1 to 1 1/2 hours front and back).
Evening hours unchanged (as far as I can see).
For the math department assessment committee.
Visit https://forms.gle/rctWLa7Rxt19RHfj8 and fill out the form.
OR get a paper copy from me, fill it out, and return it to me.
Sample questions are now available through Canvas.
Exam is next Monday, May 13, 12:00 Noon, in our regular classroom.
Comprehensive, but emphasizing material since 2nd hour exam (e.g., sets, functions, relations, infinite sets; problem sets 7 through 10).
Rules and format otherwise similar to hour exams, especially open-references rule.
2 1/2 hours but designed for about 2 hours, i.e., less time pressure
I’ll bring donuts and cider.
Thursday, May 9 (study day)
11:00 - 12:00
Fraser 213
Please bring things you want to talk about.
SOFIs are under way.
10 responses (42%) so far. Thank you!
But more responses are always helpful. I do read them and apply the feedback where possible to future classes (like the mid-semester feedback).
End of section 9.3.
Why does the proof deal with A = ∅ separately from the main argument? Because the main argument revolves around t being an element of A, which won’t happen if A is empty. Effectively, the proof has two cases, A is empty and A is not empty.
What proof strategy does the argument that there is no surjection from A to P(A) use? Contradiction, with cases within the contradiction argument (and cases outside it, as noted above).
Is it possible that the set S in the proof is empty? If so, does the proof still work?
One answer: If S were empty, then x ∈ f(x) for all x, i.e., every f(x) is non-empty, so f(x) never produces ∅. But ∅ is in P(A), so f isn’t a surjection.
Another answer: Maybe S is empty, but that just means that the second case in the contradiction argument (t ∉ S) always applies, and still leads to a contradiction.
Draw a diagram showing how the relationships between elements of A, function f, and set S lead to contradictions.
Several diagrams were concrete examples, suggesting, for example, how set S can never be the image of any element of A, or this arrow diagram emphasizing how there are too many elements in P(A) for each to be an image of a distinct element of A:
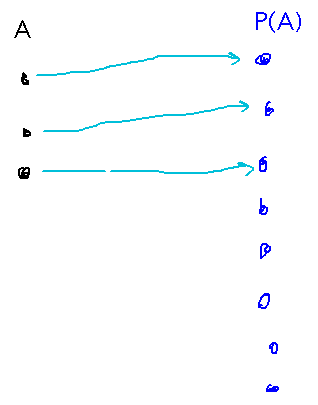
Here’s a diagram that attempts to capture key ideas from the proof, e.g., A and P(A) and a mapping of one to the other, how images of elements in A might or might not contain those elements, the set S, etc.
How many infinite cardinalities are there? Infinitely many, because you can always keep making power sets of power sets.
Are the infinite cardinalities found by this “power sets of power sets” idea all of them? No-one knows! In particular, there might or might not be infinite cardinalities between the cardinality of the naturals and that of the reals, but there seems no way to prove either choice.