SUNY Geneseo Department of Mathematics
Thursday, May 9
Math 239 01
Spring 2019
Prof. Doug Baldwin
An equivalence class for relation R is a set containing all values that are equivalent to each other.
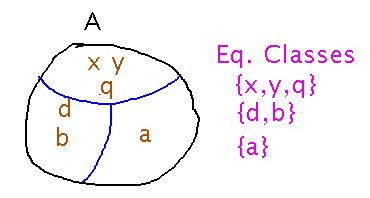
A partition of universal set U is a family of subsets of U such that all members of U are in exactly 1 subset and no subset is empty.
Theorem: the family of equivalence classes of R : A → A is a partition of A and any partition of A defines an equivalence relation on A (via an “in same partition” relation).
To prove that a set A is countably infinite: officially, find a bijection from A to the natural numbers. Practically, find a bijection between A and any countably infinite set (since the existence of bijection f means f-1 is also a bijection the direction of the bijection you find doesn’t really matter; since every countably infinite set S has a bijection, say g, to the naturals, if you find a bijection f from A to S then g ○ f is a bijection from A to the naturals).
Example: the set of multiples of 10, i.e., { 10n | n ∈ ℕ } is countably infinite. A bijection from the naturals to 10n is f(n) = 10n. Check that it’s an injection: 10n = 10m implies n = m after dividing by 10. Check that it’s a surjection: let x be any multiple of 10, i.e., x = 10n for some natural n, so x = f(n).
Prove that the union of 2 disjoint countably infinite sets is countably infinite: let A and B be disjoint countably infinite sets. Show that there is a bijection from A ∪ B to the naturals. Since A and B are countably infinite, there exist bijections f : A → ℕ and g : B → ℕ. Construct h : A ∪ B → ℕ as
(Showing that the union is countably infinite if the sets aren’t disjoint is harder, but still possible. For example, you can construct a bijection in a style similar to what we did for Cartesian products: map the first element of A -- i.e., the element x with the smallest f(x) -- to 1, then the first element of B-A -- i.e., the element y with the smallest g(y) -- to 2, then the 2nd element of A to 3, and so forth; if one set runs out, finish with the other.)
Cardinalities for common sets of numbers:
Induction hypotheses about more than just 1 number, i.e., assume P(i) for all i between the base case(s) and k, then show P(k+1).
Here’s a (literally) textbook example, but one that no-one remembered seeing before.
Theorem: every natural number n ≥ 2 is either prime or a product of primes.
Proof by strong induction.
For the basis case, suppose n = 2. 2 is prime, and so is “either prime or a product of primes.”
For the induction step, assume every natural number i such that 2 ≤ i ≤ k is prime or a product of primes for some natural k ≥ 2 (i.e., this is the assumption about P being true of multiple values, not just k). Show k+1 is either prime or a product of primes. There are 2 cases: k+1 is prime, and k+1 is not prime.
If k+1 is prime, then it’s clearly “either prime or a product of primes.”
If k+1 is not prime, it must be the case that k+1 = nm for some natural numbers n and m between 2 and k. So the induction hypothesis applies, i.e., n is a product of primes, as is m. So k+1 = nm is a product of products of primes, which is another product of primes.
(No Next Lecture)