Uncountable Sets

Return to Course Outline

Previous Lecture

Misc

Review Session

Thursday, May 9 (study day)

11:00 - 12:00

Fraser 213

Please bring things you want to talk about.

Final Exam

Monday, May 13, 12:00 Noon.

Comprehensive, but emphasizing material since 2nd hour exam (e.g., sets, functions, relations, infinite sets; problem sets 7 through 10).

Rules and format otherwise similar to hour exams, especially open-references rule.

2 1/2 hours but designed for about 2 hours, i.e., less time pressure

I’ll bring donuts and cider.

I’ll find sample questions

SOFIs

SOFIs are under way.

Please fill them out. I do read them and apply the feedback where possible to future classes (like the mid-semester feedback).

Questions?

Uncountable Sets

Section 9.3.

Dodgeball

Try it. Here’s the final configuration from one of the games, a win for red.

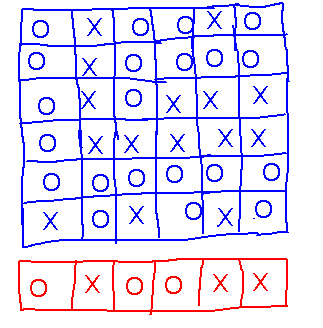
What does this have to do with uncountability? The winning strategy for red is to ensure their pattern never matches any of blue’s by making their i^th cell differ from the i^th cell in blue’s ith guess. This is the diagonal strategy used by Cantor to show that the reals must be uncountable.

Functions

Prove that the set of all functions from ℕ to ℕ is uncountable.

Proof outline: Show that it is impossible to have a bijection between the set of functions and the naturals. As with many proofs of impossibility, do this by contradiction. Specifically, assume there is a bijection, and so it associates a number with each function, i.e., the functions from ℕ to ℕ can be listed as f₁, f₂, etc. But now construct a new function, g(n) = f_n(n) + 1, which differs from each of the f_i and so is not the image of any natural number under the “bijection,” and yet g is also a function from ℕ to ℕ, and so must be the image of something.

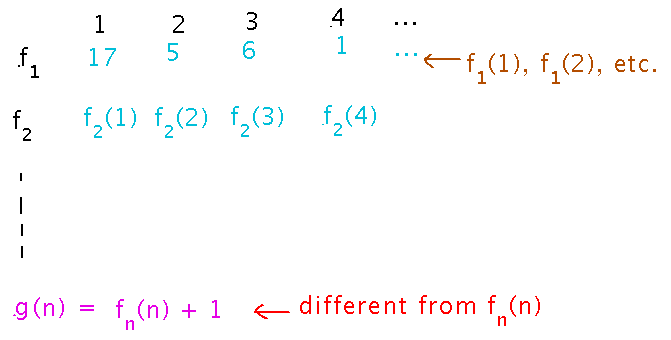
Here is the proof written formally, and its LaTeX source.

Key Points

The use of a diagonal argument to show that the reals are uncountable.

In fact, diagonal arguments can be used to show many sets are uncountable.

But so can bijections from known uncountable sets to new sets.

Strings

Define a string to be a finite-length sequence of characters, e.g., “abc”, “3.14159 + x”, etc.

Is the set of strings creatable on a computer keyboard finite, countably infinite, or uncountable?

Intuition seems to be that it’s countably infinite. Think about it over the weekend and come to class Monday ready to suggest a proof (or questions).

Next

More on countable vs uncountable sets.

Next Lecture