Countable Sets, Part 2

Return to Course Outline

Previous Lecture

Misc

Colloquium

Prof. Cesar Aguilar

“Examples in Analysis”

Thursday, May 2, 2:30, Welles 138

Extra credit for reactions/connections/reflection paragraph.

Review Session

Thursday, May 9 (study day)

11:00 - 12:00

Fraser 213

Please bring things you want to talk about.

Final Exam

Monday, May 13, 12:00 Noon.

Comprehensive, but emphasizing material since 2nd hour exam (e.g., sets, functions, relations, infinite sets; problem sets 7 through 10).

Rules and format otherwise similar to hour exams, especially open-references rule.

2 1/2 hours but designed for about 2 hours, i.e., less time pressure

I’ll bring donuts and cider.

I’ll find sample questions

SOFIs

SOFIs have started!

Please fill them out. I do read them and apply the feedback where possible to future classes (like the mid-semester feedback).

Questions?

Countably Infinite Sets

Section 9.2.

Example

Prove that the set S = { 2ⁱ | i ∈ ℕ } is countably infinite.

Ideas: We need to show there is a bijection between S and ℕ.

Pick f : ℕ → S to be f(n) = 2ⁿ.

This is an injection since if 2^a = 2^b, then a = b.

It’s also a surjection since if s is in S, then s = 2^t, so its preimage is the natural number t.

Here is a formal version of this proof, with LaTeX source here.

Key things this proof illustrates include

• If you want to show that set A is equivalent to set B, it doesn’t really matter whether you provide a bijection from A to B or vice versa.
• It’s often very easy to show that the functions involved in equivalence proofs are bijections.

Cartesian Products

Show that the Cartesian product of 2 countably infinite sets is countably infinite.

First apparent problem: the elements of a Cartesian product are ordered pairs of who-knows-what, how can you define a bijection on them?

Solution: Since the sets in question here are countably infinite, you know there are mappings between them and the naturals. So use those mappings to treat A and B as if they were the naturals themselves. (If you come up with a bijection, f, between pairs of naturals and ℕ but the input sets aren’t sets of naturals, you can easily modify your bijection to first apply functions that map A and B to ℕ, and then apply your f to those results.)

Second apparent problem: we need to associate each ordered pair with a natural number, but any way of doing that (e.g., all the pairs that start with 1, then all that start with 2, etc.) seems to have to deal with an infinite number of pairs with one coordinate before it can even consider others.

Solution: Organize pairs in a grid with rows and columns indexed by coordinate, and enumerate pairs along diagonals (or, more generally, enumerate along any paths you like, but take a few elements from one path, then switch to another, etc., so that you eventually reach any element along any path).

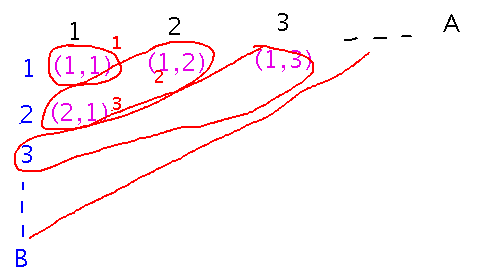
Key Point

Prove that a set is countably infinite by finding a bijection to/from the naturals.

Next

Uncountable Sets — are there such things?

Read section 9.3

Next Lecture