Misc
Colloquium tomorrow (Thursday, April 25), 2:30 - 3:30, Welles 138
Prof. Sedar Ngoma
“An Introduction to Finite Difference Methods”
Extra credit for reflection/connection paragraphs.
Questions?
Equivalence Classes and Partitions
Section 7.3
Examples
Consider the relation ~ on the reals defined by x ~ y if and only if sinx = siny. (~ is an equivalence relation.)
What is [0]?
“[0]” is the equivalence class of 0, i.e., the real values x such x ~ 0, i.e., such that sinx = sin 0
In set-builder notation, [0] = { nπ | n ∈ ℤ }
Define relation R on {0,1,2,3} by a R b if and only if a ≡ b (mod 2). List all the distinct equivalence classes.
{1,3} = [1] = [3]
{2,0} = [2] = [0]
Do they form a partition of {0,1,2,3}? Yes, they divide {0,1,2,3} into disjoint subsets that collectively contain every element of {0,1,2,3}, with no empty subsets:
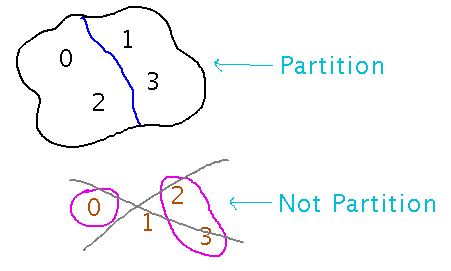
Proofs
Here’s an indexed family of sets: A = {Ai | 1 ≤ i ≤ 9 } where Ai = { x ∈ {1,2,3, ..., 99} | the first digit of x is i }. For example, A1 = {1,10,11,12,13,14,15,16,17,18,19}.
Prove that A forms a partition of { 1, 2 ,3, ..., 99 }.
The basic idea behind such proofs is to proof that the family of sets satisfies all the requirements for being a partition (every element of the universal set is in one member of the family, the members are disjoint, and none is empty). Here is the formal proof, and here is its LaTeX source.
Now that we know A defines a partition, is “starts with the same digit” an equivalence relation on base-10 integers between 1 and 99? Yes, because every partition corresponds to an equivalence relation and vice versa.
Key Points
Definition of equivalence class.
Definition of partition.
Proving that a family of sets is a partition.
Relationship between equivalence classes and partitions.
Last Problem Set
See handout for details.
Next
How big is [0] from the “x ~ y if and only if sinx = siny” example above?
Look at exactly what it means for a set to be finite.
Read section 9.1