Uncountable Sets

Misc

Sample Final

See “Sample Final.pdf” document in Canvas, available in “Review” module.

Review Session

Study day (Wednesday May 2), 3:30 - 4:30, in our usual classroom.

Final Exam

Thursday, May 3, 12:00 noon to 2:30 PM, in our regular room.

Comprehensive, but with an emphasis on material since the 2nd hour exam (e.g., induction, sets, functions, relations, infinite sets).

Designed to be 2 to 2 1/2 times as long as the hour exams, but you have 3 times as much time.

Rules and format otherwise similar to hour exams, especially the open-references rule.

I’ll bring donuts and cider.

SOFIs

7 have been done as of this morning. Thank you!

They are useful to me in improving courses for the future, and thus useful to you if you ever take another course with me (and you get 1 printing dollar per SOFI), so please fill them out.

Post-Course Assessment

Questions?

Uncountable Sets

Section 9.3.

Key Idea

Play the “dodge ball” game from the reading:

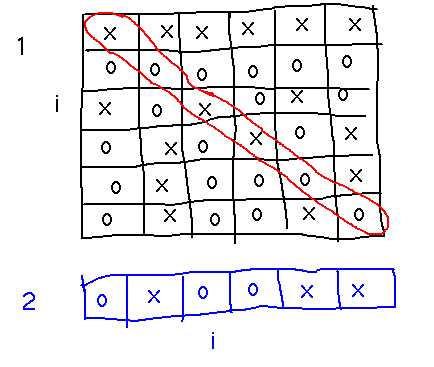
What does the game have to do with anything else in the reading?

It’s a model for how given a list of numbers, you can make a new number different from all because it differs from the i^th in its i^th digit.

Thus, since decimal representation can use countably infinitely many digits, any list of countably infinitely many real numbers must leave at least one real out.

Therefore the reals (between 0 and 1) are uncountably infinite.

This is the gist of Cantor’s diagonalization proof.

A similar idea also shows that there can’t be a bijection between a set and its power set.

Which implies that there are “infinitely many infinities.”