SUNY Geneseo Department of Mathematics
Friday, April 27
Math 239 01
Spring 2018
Prof. Doug Baldwin
Study day (Wednesday May 2), 3:30 - 4:30, in our usual classroom.
Thursday, May 3, 12:00 noon to 2:30 PM, in our regular room.
Comprehensive, but with an emphasis on material since the 2nd hour exam (e.g., induction, sets, functions, relations, infinite sets).
Designed to be 2 to 2 1/2 times as long as the hour exams, but you have 3 times as much time.
Rules and format otherwise similar to hour exams, especially the open-references rule.
I’ll provide a sample from a past semester.
I’ll bring donuts and cider.
3 have been done as of this morning. Thank you!
They are useful to me in improving courses for the future, and thus useful to you if you ever take another course with me (and you get 1 printing dollar per SOFI), so please fill them out.
Section 9.2.
Prove that the set T = { 2i | i ∈ ℕ } (informally, “the powers of 2”) is countably infinite.
Definition: a set is countably infinite if and only if it is equivalent to (i.e., has a bijection to) the natural numbers.
We can create a bijection between naturals and powers of 2 based on the following correspondence:
| Natural Number | Power of 2 |
|---|---|
| 1 | 2 (= 21) |
| 2 | 4 (= 22) |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
| ... | ... |
While some countability/uncountability proofs are based on correspondences defined tabularly or visually, and shown to be bijections in relatively informal terms, this one allows the bijection to be defined more formally, which I do in the following proof:
Proof: We prove that set T is countably infinite by showing a bijection between it and the natural numbers. In particular, the function f(n) = 2n is a bijection between the naturals and the powers of 2, because it is injective (if f(n) = f(m) then 2n = 2m and so n = m) and surjective (any element of T, call it 2x where x is any natural number, is the image of x under f). Since f is a bijection from naturals to T, f-1 is a function and also a bijection from T to naturals. We have thus proven that set T is countably infinite. QED.
Notice that this proof focuses on a bijection from naturals to powers of 2, which is technically the opposite of what we need. But as explained in the second-to-last sentence of the proof, having a bijection from set A to set B also provides a bijection from B to A since bijections always have inverses which are also bijections. So it’s common in proofs about equivalence between infinite sets to not be terribly concerned about which way the bijection you construct goes.
Why can every countably infinite set A be written as A = { a1, a2, ... } , i.e., as a list of elements indexed by natural numbers?
Because being countably infinite ensures there’s a one-to-one correspondence (i.e., a bijection) between elements of A and natural numbers, and that correspondence can be used to provide the subscripts.
Prove that if A and B are countably infinite sets, then A × B is countably infinite.
The key idea is to think of the Cartesian product as a table, and associate ordered pairs from A × B with natural numbers along diagonals of the table, thus:
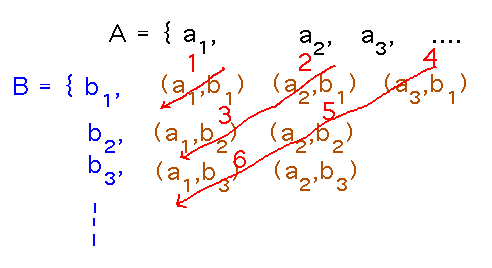
Figure 1.
As a more formal proof, this idea becomes...
Proof: We show that if A and B are countably infinite sets, then A × B is countably infinite by establishing a bijection between A × B and the natural numbers. The bijection corresponds to associating natural numbers with pairs in A × B as shown in Figure 1. Every pair lies on some diagonal, and the process of associating pairs with naturals will eventually reach that diagonal, so the association is surjective. Further, the process only assigns each natural number to a pair once, so it is injective. Thus the association in Figure 1 is a bijection, which establishes that if A and B are countably infinite sets, then A × B is countably infinite. QED.
Prove sets are countably infinite by finding bijections to the naturals.
Uncountable sets.
Read section 9.3.