SUNY Geneseo Department of Mathematics
Wednesday, April 11
Math 239 01
Spring 2018
Prof. Doug Baldwin
Next Tuesday, April 17.
Extra credit for writing a short reaction to any one math-related event (similar to extra credit for colloquia).
Section 6.1.
Which of the following can be graphs of functions from ℝ to ℝ? What about functions from subsets of ℝ to ℝ? What do you estimate the domains and ranges to be? What can you suggest as codomains?
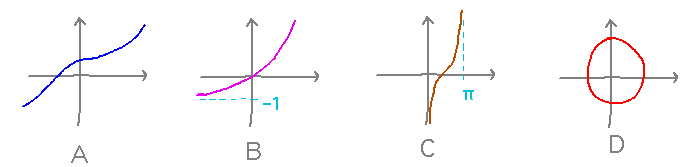
A: This is a function with domain (-∞,∞) aka ℝ, because it maps every real number to some value. The range is also (-∞,∞), as is the codomain. (But notice that the function needn’t map something to every member of the codomain, so the codomain could also be any set that contains the range, ℝ, as a subset.)
B: This is also a function, with domain = (-∞,∞), range = (-1,∞), and codomain = (-∞,∞). This is an explicit illustration of a case where the range and codomain aren’t the same. We could identify this function as B: ℝ → ℝ.
C: This is a function, but not on ℝ, only on (0,π). Part of the definition of a function is that it maps every element of the domain. So we cannot describe C as C: ℝ → ℝ. This function’s range is (-∞,∞).
D: This isn’t a function at all, it would have to map most x values to 2 y values.
Similar questions for finite sets from progress check 6.4.
The key ideas are that to be a function, a mapping still has to map every element of its domain (not just some), and each can only map to one element of the codomain. These ideas apply to functions on small finite sets as well as to functions on the more familiar infinite sets.
Does this notion of function accommodate multivariable functions?
e.g., area for rectangles of width x and height y, A(x,y) = xy
Yes, because we can take the domain of such a function to be a Cartesian product, e.g., A : ℝ* × ℝ* → ℝ, where ℝ* = { x ∈ ℝ | x ≥ 0 } aka the non-negative reals.
Functions can also map between sets of very different sizes, thanks to the fact that multiple elements of the domain can map to the same element of the codomain. For example, the “floor” function (⌊ x ⌋) is the largest integer less than or equal to real number x, i.e., floor maps from the reals to the integers.
For example, differentiation is a function from (differentiable) functions to functions.
Definite integration is a function from ℝ x ℝ x (integrable) functions to ℝ.
But indefinite integration isn’t a function, because each integrable function has many antiderivatives.
Someone suggested that the circular graph (graph D) earlier could represent a union of two functions. But that suggests that functions are sets that you can take unions of. And in fact, the set-theoretic definition is that a function is a set of ordered pairs, (input, output). (But this definition still requires that each element of the domain only map to one element in the codomain, i.e., that for each element of the domain exactly one pair has that element as its first coordinate, so while the union of a function whose graph is the upper half of a circle with a function whose graph is the lower half is well defined as a set, it isn’t a function.)
Terminology and definitions related to functions.
Arrow diagrams as a way to display discrete functions visually.
Lots of unusual things are actually functions.
Some important and common kinds of function.
Read section 6.3.