SUNY Geneseo Department of Mathematics
Friday, April 13
Math 239 01
Spring 2018
Prof. Doug Baldwin
Section 6.3.
Identify the following graphs as (plausibly) being injections, surjections, bijections, and/or none from ℝ to ℝ:
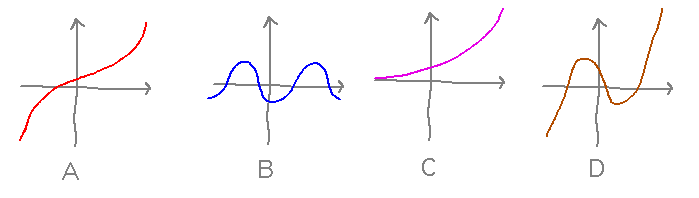
A: injection (one-to-one, i.e., every x value maps to a distinct y value) and surjection (onto, i.e., every element of the codomain is the image of some element of the domain) therefore bijection (both).
B: Neither (some reals aren’t images of any x, many x values map to the same y value).
C: injection, not surjection (but this is a surjection from the reals to the positive reals -- how you define the codomain matters!)
D: surjection (all reals are images of some x, but many x values map to the same y).
Consider f : ℕ → ℕ defined by
Prove that f is a surjection.
Idea: show that every natural number x is f(n) for some natural n.
Proof: We show that f is a surjection by showing that every natural is the image under f of some other natural. Let x be any natural number. Then 2x is even and natural, and so f(2x) = 2x/2 = x. We have thus shown that every natural number is the image of some other natural under f, and thus that f is a surjection. QED.
Show that f is not an injection.
We can do this by simply showing an example in which f(x) = f(y) for two distinct natural numbers x and y. For instance, f(1) = 1 = f(2).
Now consider g : ℕ → ℕ defined by
Prove that g is a bijection.
To prove that a function is a bijection, prove that it is a surjection and an injection.
It turns out that there are several places in the proof where it is helpful to know about the relationship between the oddness or evenness of n and the oddness or evenness of g(n). So start with the following lemma:
Lemma 1: g(n) is odd if and only if n is even.
Proof: We prove that g(n) is odd if and only if n is even by proving each direction of the biconditional.
First, assume that n is even, i.e., n = 2k for some integer k. Then g(n) = n - 1 = 2k-1 = 2(k-1)+1, which is odd since k-1 is an integer by closure under subtraction.
For the other direction, we prove the converse, i.e., that if n is odd then g(n) is even. So assume that n is an odd natural number, i.e., n = 2k + 1 for some integer k. Then g(n) = n + 1 = (2k+1) + 1 = 2k + 2 = 2(k+1), which is even.
We have now proven that g(n) is odd if and only if n is even. QED.
Now we prove the main claim, that g(n) is a bijection.
Proof: We prove that g is a bijection by proving that it is a surjection and an injection.
We prove that g is an injection by showing that if g(x) = g(y) then x = y. Assume g(x) = g(y) = k, for some natural number k. We then consider two cases, namely that k is odd and that k is even. If k is odd, then, by Lemma 1, x and y must both be even. Therefore g(x) = x - 1 and g(y) = y - 1. Since both are equal to k, x - 1 = y -1, from which we see that x = y. In the case that k is even, Lemma 1 tells us that x and y are both odd. Thus g(x) = x + 1 and g(y) = y + 1. We now see that x + 1 = y + 1, and so that x = y. In both cases, g(x) = g(y) implies that x = y, and so we conclude that g is an injection.
We prove that g is a surjection by showing that every natural number n is the image of some other natural under g. So let n be an arbitrary natural number, and again consider two cases, n is even and n is odd. If n is even, then it can only be the image some odd number, by Lemma 1. Indeed, consider n - 1. For all even naturals n, n - 1 is greater than or equal to 1 and so is in the domain of g. Further, n - 1 is odd. Thus we can apply g to n - 1, getting g(n - 1) =n - 1 + 1 = n. Thus every even natural number is the image of some natural under g. Similarly, if n is odd, then n + 1 is even and natural, and g(n + 1) = n + 1 - 1 = n. Thus every odd natural number is also the image of some natural under g. Since both the even and odd natural numbers are images of other naturals under g, we conclude that g is a surjection.
Having shown that g is both an injection and a surjection, we have shown that g is a bijection. QED.
The definitions of injection, surjection, and bijection.
Methods for proving that functions are injections, surjections, and bijections.
Compositions of functions
Read section 6.4.