Strong Induction

Misc

Exam 2

Hour exam 2 is next Wednesday, March 28.

It will cover material not covered on the first exam, through (at most) simple induction (e.g., quantifiers, proof via the contrapositive, proofs about biconditionals, proof by contradiction, proof in cases, maybe some induction).

The rules and format will otherwise be similar to the first exam, particularly the open-book, open-computer rule.

GROW STEM Talk

“Oh, the Places You Will Go”

(Identifying and mapping career trajectories and facilitators)

Dr. Amanda C. Bryant-Friedrich

Monday, March 26, 5:30 - 6:30 PM, Newton 204.

Questions?

Strong Induction

Strong induction, otherwise known as the 2nd principle of mathematical induction.

Recap: What Strong Induction Looks Like

Outline of a proof of P(n) using strong induction (differences from standard, or weak, induction in red):

1. Base case(s). Prove P(1) (and maybe P(2), P(3), ...)
2. Induction step
   1. Prove that if P(1), P(2), ..., P(k) are all true, then P(K+1) is true

Proposition 4.11

Progress Check 4.10 / proposition 4.11: for all natural numbers n ≥ 8, there exist non-negative integers x and y such that n = 3x + 5y.

Proof: We prove by strong induction on n that for all natural numbers n ≥ 8, there exist non-negative integers x and y such that n = 3x + 5y.

For the base cases consider n=8, n=9, n=10. Each is of the desired form, namely...

• 8 = 3×1 + 5×1
• 9 = 3×3 + 5×0
• 10 = 3×0 + 5×2

For the induction step, we assume that 8, 9, 10, ..., k can be written in the form 3x + 5y for non-negative integers x and y and for some k ≥ 10 and show that k+1 can be written in the form 3z + 5w for non-negative integers z and w. Notice that k+1 = (k-2) + 3, and that 8 ≤ k-2 ≤ k. Therefore there are non-negative integers x and y such that

Adding 3 to both sides gives

showing that k+1 is of the form 3z + 5w where z = x+1 and w = y; both are non-negative integers since x and y are and adding 1 to a non-negative integer produces another non-negative integer.

We have now shown by strong induction that for all natural numbers n ≥ 8, there exist non-negative integers x and y such that n = 3x + 5y. QED.

There are some subtle points in this proof (and in many proofs by strong induction):

• The base cases and the induction hypothesis are carefully coordinated so that the induction step “connects” to the base cases even for the smallest possible value of k.
• The realization that k+1 can be handled as k-2 (to which the induction hypothesis applies) plus 3 is the core insight in the proof.
• Even though there are 3 base cases, only 1 induction step is necessary, it draws on each of the base cases for different values of k+1:

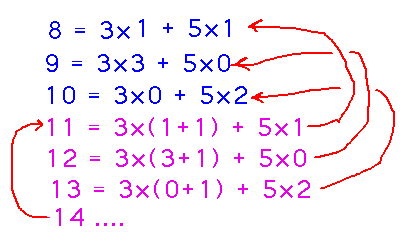
Next

Arithmetic Expressions. Consider the following definition and questions for a preview of what we’ll do Friday (March 23):

Define a “fully parenthesized arithmetic expression” to be a string of one of the following forms:

• C where C is a natural number written in conventional base-10 notation, i.e., a constant.
• (E₁) + (E₂), (E₁) - (E₂), (E₁) × (E₂), or (E₁) ÷ (E₂) where E₁ and E₂ are fully parenthesized arithmetic expressions. The symbols +, -, ×, and ÷ are called “operators,” and are the only operators.

Step 1

Give some examples of fully parenthesized arithmetic expressions.

Step 2

Prove that for all integers n ≥ 0, every fully parenthesized arithmetic expression with n operators has n+1 constants.