Families of Sets

Return to List of Lectures

Previous Lecture

Misc

I’ll be out of town next Friday (April 7). Class will be taught by Prof. Reuter.

Questions?

Indexed Families of Sets

Basic Ideas

Let A₁ = { a, b, c, d }, A₂ = { a, e, i, o, u, y }, A₃ = { x, y, z }

What is the union of the A_i for 1 ≤ i ≤ 3? What about the intersection?

Relevant ideas or questions from the reading

• Union and intersection generalize in “natural” ways to more than 2 sets.
• The union of sets A_i is the set of elements that are in any one (or more) of the A_i.
• The intersection of sets A_i is the set of elements that are in every one of the A_i.

Answers



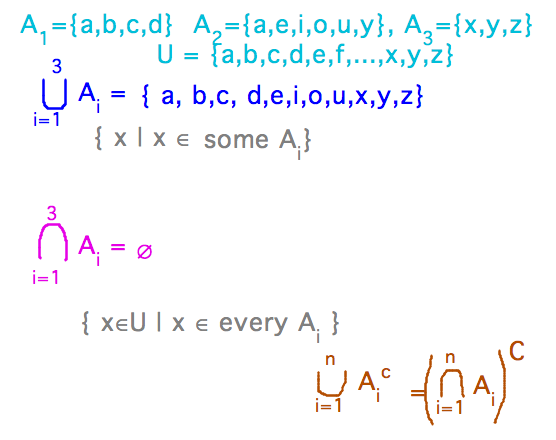
Comments

• The informal ideas that union is the things in any of the sets and intersection the things in all the sets scales up to as many sets as you want (including infinite numbers).
• Notice that even laws such as De Morgan’s scale too.
• Note the notation for union and intersection over a range of indices, you’ll probably see it again.

Families and Indexing Sets

What is the indexing set for the family of sets described above? How might you name that family and what would you write to define the name?

Answers



Comments

• An indexing set is kind of like a universal set for indexes.
• Families of sets are often defined via an index from which the elements of each member of the family can be calculated, as in the 2n, 4n, 6n example above.

Progress check 5.32, part 3

Given that C = { C_n | n ∈ ℕ } and C_n = (n,∞), is C disjoint? How about pairwise disjoint? The universal set here is the set of real numbers.

Relevant ideas or questions from reading

• For a pair of sets, A and B are disjoint means A ∩ B = ∅
• A family is disjoint if the intersection over the whole family is empty

Answer

• The family is disjoint unless there is some real number that is in all members. But for every real number x, there is some natural number n such that n > x (this comes from some of the “proofs out of context” ideas we have been using), and so x is not in C_n. Thus every real number is not a member of some members of the family, and so the family is disjoint.

Comments

• Note that pairwise disjoint means that every pair of members of the family has an empty intersection.
• For this example, C_n and C_m have a non-empty intersection for all n and m, because there is always a real number x greater than both n and m, and thus x ∈ C_n ∩ C_m.

Next

Functions

Read textbook sections 6.1 and 6.2

Next Lecture