Misc
Colloquium
“Structure and Symmetry: An Introduction to Lie Algebras and Representation Theory”
By Chad Magnum, Niagara University
Friday, April 7, 2:30 PM, Newton 203
Extra credit as usual for writing a paragraph or so about connections you make to the talk.
Random Names
Would random names be less stressful if you could email me reading summaries before class?
- If I receive your email at least 15 minutes before class and your name comes up for a reading summary, I’ll use the email anonymously for the summary rather than calling on you.
- But if I need to use the random names to start discussion of an in-class problem (relatively rare) you might still get called on.
Questions?
Functions
Reading
Sections 6.1 and 6.2
Terminology. Consider the functions sinx and tanx. What are the domains? Codomains? Ranges?
For sinx, what is the image of π/2? What is the set of preimages of 0?
Relevant ideas or questions from reading
- A function is a mapping from one set to another, e.g., f : A → B means f maps A into B. Two things in A can map to the same member of B.
- A is the domain
- B is the codomain
- An image is a member of B, and a preimage is member of A
- Image and preimage are in some sense opposites: an image is output from the function, while a preimage is input to the function
- Range corresponds to image; in particular the range is the set of all images
- A function’s range is the set of values f(x) where x is in A, which can be a more limited set than the codomain
- Specifically, the range is a subset of the codomain
- Codomains can be chosen for convenience or clarity in a particular problem context, as long as they contain the actual range
- When y = f(x), y is in the codomain and range, x is in the domain. y is the image of x and x is a preimage of y.
- Writing functions? Consider language such as “let f : ℝ → ℝ where f(x) = ....”
Solutions to the questions about sinx and tanx
- sinx: The image of π/2 = 1, the preimages of 0 are the members of { kπ | k ∈ ℤ }, the domain = ℝ, the range = [-1,1]. The codomain can be any subset of ℝ that contains [-1,1]
- tanx: The domain has to exclude reals where tanx is undefined. So domain = ℝ except for odd multiples of π/2, i.e., (2n-1)π/2 where n is an integer
- A more symbolic way of describing the domain would be { y ∈ ℝ | y ≠ (2n-1)π/2 where n ∈ ℤ }
- Or ℝ - { (2n-1)π/2 | n ∈ ℤ }.
- The codomain = the range = ℝ
Comments
- A lot of what is important here is the definitions of terms, as given in the reading summary
- Preimages aren’t unique, you can talk about sets of preimages.
- Images are unique, and their uniqueness is an important part of the definition of “function”
- A function has to be defined on every member of its domain. This is part of the definition of domain.
Constructing functions and non-functions.
Let A = { a, b, c, d }, B = { w, x, y, z }
Give an example of an association between elements of A and elements of B that is a function from A to B. Given an example of an association between elements of A and elements of B that is not a function from A to B. Draw arrow diagrams of both associations.
Relevant ideas or questions from reading
- See the textbook for examples of arrow diagrams
- Arrow diagrams are useful when a function’s domain and codomain are small
Solutions
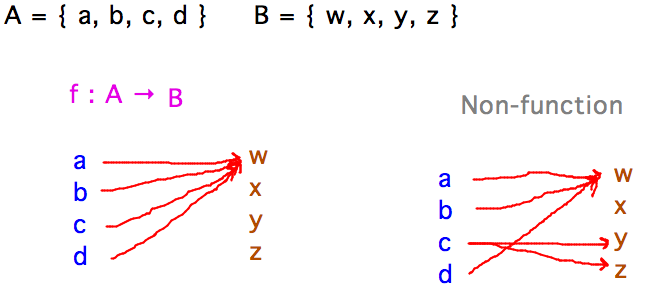
Comments
- The basic form of an arrow diagram is some representation of the elements of the domain and codomain, with arrows directed from each x in the domain to f(x) in the codomain.
- Functions necessarily have exactly one arrow out of each member of the domain - if there are no arrows, or more than one, from some member of the domain then it’s not a function.
Functions as Sets
Notice that arrow diagrams can be read as defining ordered pairs of domain elements with their images under some function.
For example, the function f shown above consists of the following ordered pairs:
- f = { (a,w), (b,w), (c,w), (d,w) }
This is the set theorist’s definition of “function” - a set of ordered pairs that forms a subset of the Cartesian product of the domain and codomain.
Problem Set
See handout.
Next
Some important kinds of function
Read textbook section 6.3