Misc
I will be out of town next Friday (April 7). Plans for class that day will be announced soon.
My solutions to problem set 9 are on Canvas in LaTeX and PDF form.
Questions?
Recurrence relation from Problem Set 10?
The recurrence relation:
- f(n) = 1 if n = 1
- f(n) = 2 + f(n-1) if n > 1
Problem: prove f(n) = 2n - 1.
Use induction.
Basis step is n = 1.
Inductive step proceeds just like in other inductions: assume P(k), show P(k+1)
The two proofs in question 3?
The two forms of proof are via logical definitions of set operations, and via set algebra
Cartesian Product
Basic Definitions
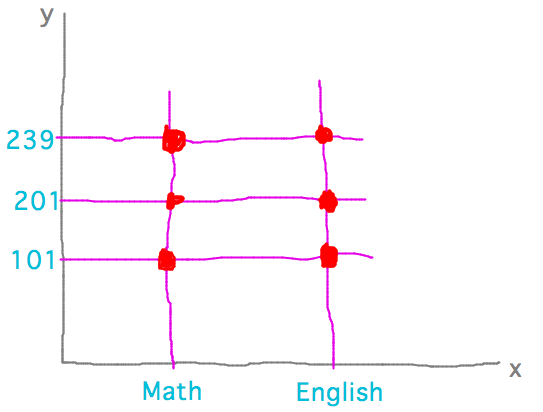
Imagine a set of subjects, S = { Math, English } and a set of numbers, N = { 101, 201, 239 }.
What is S × N?
How about N × S?
Relevant ideas or questions from the reading
- Cartesian products are mappings of sets onto axes, e.g., S × N maps S to x axis and N to y, or the opposite mapping for N × S
- Definition: S × N = { (x,y) | x is in S and y is in N }
- i.e., the set of all ordered pairs of members of S and N
So S × N = { (Math,101), (Math,201), (Math,239), (English,101), (English,201), (English,239) }
N × S = { (101,Math), (101,English), (201,Math), (201,English), (239,Math), (239,English) }
Comments
- The idea of Cartesian product as putting the sets along axes provides an interesting way to visualize the product:
Properties
Conjecture: | A × B | = |A| |B|
Prove this by induction on the size of B.
- Basis: |B| = 0, i.e., B = {}. There are no pairs from A and B, so |A × B | = 0 = |A| × 0 = |A| |B|.
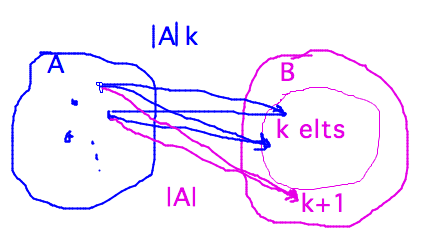
- Inductive step: Assume that |A × B | = |A| |B| when |B| = k, show |A × B | = |A| |B| when |B| = k+1. Consider pairing elements of A with the first k elements of B. This is A× B′ where B′ is a k-element subset of B. By the induction hypothesis, this set has cardinality |A|k. There are |A| additional pairs to make with the (k+1)th element of B, so the total number of pairs in A × B is |A|k + |A| = |A|(k+1) = |A||B|.
An illustration of the pairings of elements from A and B in the inductive step:
In the course of proving this, we also realized a couple of other things about Cartesian products, namely...
- A × ∅ = ∅
- A × B is not always disjoint from B × A. Consider the counterexample A = {1,2}, B={2,3}, then (2,2) appears in both A × B and B × A.
Does FOIL work for Cartesian products, e.g., is (A ∪ B) × (C ∪ D) = A×C ∪ A×D ∪ B×C ∪ B×D?
Yes, as can be shown by twice using the fact that Cartesian product distributes over union.
Relevant ideas or questions from the reading
- There are algebraic laws for Cartesian products, including many distributive laws
- These laws can be used to do proofs about equalities involving Cartesian products
Next
Indexed families of sets.
Read textbook section 5.5.