Misc
Exam 2
Next Wednesday, March 8
Covers material since the first exam, mainly proof techniques (e.g., contrapositive, biconditionals, contradiction, cases, induction) but maybe also contexts such as congruence. See chapters 3 and 4, and problem sets 5 - 8.
Expect 3 - 4 questions, probably focusing more on proofs than in exam 1. Otherwise similar in style and rules to exam 1, especially open-references but closed person.
Questions?
The Second Principle of Mathematical Induction
Also known as strong induction
Example (from the book)
Theorem: Every natural n ≥ 2 is either prime or a product of primes
Proof by strong induction (aka the 2nd principle).
Basis case: 2 is prime. This establishes the basis case.
Inductive step: The goal is to prove that if 2, ..., k are either prime or products of primes, then k+1 is either prime or a product of primes. Assume 2, ..., k are either prime or products of primes, and consider k+1.
Case 1: k+1 is prime, in which case it is certainly either prime or a product of primes.
Case 2: k+1 is not prime. Then k+1 = ab where 1 < a,b < k+1, i.e., 2 ≤ a,b ≤ k, so the induction hypothesis applies to a and b. In other words, a and b are either prime or products of primes. Therefore k+1 = ab is a product of primes.
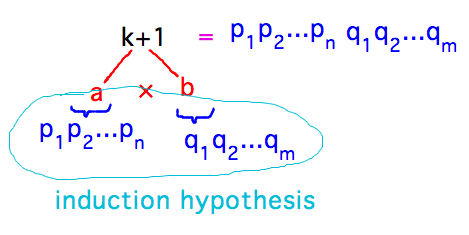
This establishes the induction step.
By the second principle of mathematical induction, we have shown that every n ≥ 2 is either prime or a product of primes. QED
Example: prove that the nth Fibonacci number is less than 2n.
The Fibonacci numbers are the sequence
- F1 = 1
- F2 = 1
- Fn = Fn-2 + Fn-1 for all n > 2
Basis step: F1 = 1 < 21 = 2; F2 = 1 < 22 = 4
Note that because the induction step is going to rely on Fk and Fk-1, we need both 1 and 2 in the basis step, so that the induction argument will be valid when k+1 = 3. This is essentially the thing that was missing in the horses proof from last class.
Induction step: assume Fi < 2i for all 1 ≤ i ≤ k, and show that Fk+1 < 2k+1. Fk+1 = Fk + Fk-1 < 2k + 2k-1....
Try to complete this proof for Monday’s class.
Next
Finish induction, particularly the proof about Fibonacci numbers, and some examples of the extended principle of mathematical induction.