Misc
Colloquium
Eleni Panagiotou, faculty candidate
“Quantifying Entanglement in Physical Systems”
Thursday, March 2, 2:30 PM, Newton 203
Extra credit for writing a paragraph or so summarizing connections you make between the talk and your own interests.
My Hectic Schedule
Starting with problem set 8, if you can demonstrate by the “complete by” date that there are no appointments left in the grading window, I’ll extend the deadline for you to the earliest date on which you can make an appointment.
Exam 2
Next Wednesday, March 8
Covers material since the first exam, mainly proof techniques (e.g., contrapositive, biconditionals, contradiction, cases, induction) but maybe also contexts such as congruence. See chapters 3 and 4, and problem sets 5 - 8.
Similar in style and rules to first exam, especially open-references but closed person. Questions will probably focus more on proofs though. 3 - 4 questions.
Next Week in General
I’m out of town from Wednesday afternoon through the end of the week.
Friday class will (probably) be something with Nicole, but the details are still being worked out.
Questions?
Induction Examples
First Example
Prove that for all natural numbers n, 2n is even.
Predicate P: P(n) is “2n is even”
Base case: Put 1 into the predicate, i.e., show P(1) is true (1 is in truth set of P). P(1) is “21 is even,” i.e., “2 is even” which is true. So the base case is now done.
Inductive step: prove that if k is in the truth set of P, then k+1 is in that truth set. Assume P(k) is true, i.e., 2k is even. P(k+1) = “2k+1 is even” which is true because 2k+1 = 2 × 2k. 2 and 2k are both even (by the induction hypothesis) so their product is even.
Understanding Induction
People (or Domino) Model. Assign each person a number to prove the proposition true of.
Most people can simply use the same general argument the others did, using the fact that the previous person showed that the proposition is true of their number. This is the induction step.
But one person doesn’t have a previous person to rely on, and so has to come up with a different argument. This is the base case.
Can the P(k) Implies P(k+1) Chain Break Down? Yes, in a proof that doesn’t really work.
For example, here’s a proof that all horses are the same color.
More formally, the proof says that in any set of n horses, all of the horses are the same color. The proof is by induction on n. The base case is n = 1, and observes that if you have only one horse it is of course the same color as itself. For the induction step, assume that all the horses in any set of k horses are the same color, and consider a set of k+1 horses. If you temporarily take one horse away, you have k horses left, and so they must all be the same color. Now bring the removed horse back, and remove another. You still have a k horses, who are all the same color. In particular, horse number k+1 must be the same color as the other horses, who are all the same color as each other.
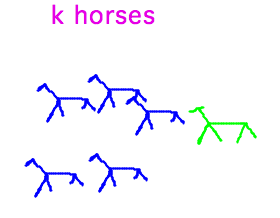
What’s wrong with this proof? The argument that horse k+1 is the same color as the other k relies on k being at least 2. You need one of the k horses to take away, and another to stay behind and “force” horse k+1 to have a certain color. But the base case is for n = 1, and so the “k implies k+1” chain breaks down where it has to connect to the base case.
Next
Variations on induction
Read section 4.2